Holas!
Mi nombre es Damián, y soy profesor (ayudante de primera) de la materia Análisis Matemático II en la UTN FRBA.
Creé este blog con la idea de publicar ejercicios y responder dudas a quienes estén cursando la materia.
WordPress permite insertar código LaTeX (ejemplo: 
No duden en participar y dejar comentarios, todas las dudas / sugerencias / correcciones son bienvenidas! 😉
| Juani Rigada en 2º Parcial Curso de Verano… | |
| Santiago Orlando en Final 19/12/2017 | |
 | damidami en Final 12/12/2017 |
 | Rochas (@agustinroch… en Final 12/12/2017 |
| Emy Goicoechea en Final 12/12/2017 | |
| damidami en Final 20/07/2010 |
| Rochas (@agustinroch… en Final 20/07/2010 |
| Rochas (@agustinroch… en Final 19/07/2011 |
| damidami en Final 19/07/2011 |
| Rochas (@agustinroch… en Final 19/07/2011 |
| damidami en Final 21/12/2009 |
| Guido Paolini en Final 21/12/2009 | |
| damidami en Tp 3 Ej 3.c |
| Guido Paolini en Tp 3 Ej 3.c | |
| Matias Isturiz en Final 24/05/2017 |
En los comentarios podés escribir expresiones matemáticas usando código 
.
Por ejemplo si escribís...
$latex 2 \int_0^4 dx \int_0^8 dz = 64 $
...se visualiza como:
Más información (en inglés)
Análisis Matemático II 
¿Habria posibilidad de agregar horarios para clases de consulta, a partir de las 18:00 hs? ya que las parsonas que trabajamos, se nos complica poder asistir en los horarios ahora pautados. Muchas gracias
Hola Maria Laura,
La verdad que ahora no estoy al tanto de cuando son las clases de consulta.
Supongo que eso lo tenés que averiguar en la UDB Matemática, o a lo mejor en el CEIT también saben.
Saludos,
Damián.
Hola Damián!
habrá alguna posibilidad de que hagas este ejercicio? (lo que menos se entiende es como plantear los límites de integreación para Stokes)
Dado f(x,y,z) = (xz – 5 sen(y), h(x,z), -x cos(y-2) con h campo escalar .
Sea C la curva definida como intersección de las superficies de ecuaciones:
y = raiz (x^2 + 4 z^2)
y = 6 – x^2 – 4 z^2
Calcular la circulación del campo a lo largo de la curva C . Indique en un gráfico la orientación elegida para la curva.
Muchas gracias!
Saludos
Alejo
Hola Alejo,
, para plantear los límites de integración conviene usar una variante de coordenadas polares, acá está la resolución:
Como la curva es una elipse en el plano
Saludos,
Damián.
damian, te planteo el siguiente problema tomado de los finales enviados por la profesora Estela:
Calcular el trabajo del campo de fuerzas f(x,y,z) = (x, y-z, -y) sobre una partícula cuya trayectoria es la curva C definida como intersección de las superficies de ecuaciones:
y=x^2
z=x
con -2<=y<=1 , sabiendo que su vector velocidad tiene componente y positiva
ya de entrada se ve que la y no puede tomar valores negativos, sin embargo el enunciado dice lo contrario.
por otro lado, si la parametrizacion fuera C(t) = (t, t^2, t)
para buscar el intervalo de t se hace:
-2 <= t <= 1
o
-2 <= t^2 <= 1 en cuyo caso t estaria entre -raiz(2) y 1, que no es un valor R
por lo tanto, no me cierra como obtener la parametrizacion de la curva con su respectivo intervalo para la variable t
te agradeceria si pudieras comentarme como resolverlo
gracias
gabriel
Hola Gabriel,
y por otro lado 
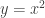con lo cual sabemos que 
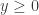, finalmente el intervalo queda 
Estoy de acuerdo con vos, para mi hay un error de tipeo en el enunciado. De todas formas lo podemos interpretar de la siguiente manera:
Si dice que
El resto aparentemente es simplemente aplicar la fórmula de circulación.
Saludos,
Damián.
Hola Damian :
Tengo dudas con el siguiente ejercicio de un parcial:
HAllar las lineas de campo de f(x,y) = (x-y, x+y); la duda basicamente es como se resuelve la ec diferencial:
y` = (x+y) / (x-y) se puede hacer por variables separables ?¿
Hola Francisco,
).
Esa ecuación diferencial no es de variables separables (diréctamente), sino que se trata de una ecuación diferencial homogénea de 1º orden (convertible a variables separables con la sustitución
Acá está la explicación de las ecuaciones diferenciales homogéneas:
Y acá está la resolución de esa ecuación diferencial:
Saludos,
Damián.
Damian, este es el final del miércoles 10/02/10.
Podes poner el resuelto del mismo? Gracias!
Hola Javier,
Vi un poco tarde tu mensaje (no se porqué no me está andando el envío automático de email cuando publican comentarios).
Con respecto al final, este mes estoy un poco complicado de tiempo para resolverlo, en la medida que pueda voy a intentar resolverlos, por lo pronto resolví sólo el primero, pero lo publico por si a alguien le sirve tener el enunciado. Está acá:
Te animás a subir la resolución de alguno como un comentario?
Cualquier otra duda mas puntual no dudes en preguntar,
Saludos,
Damián.
Hola Damián, curso con la prof Erika Guzman Yañes y estoy por rendir el integrador el jueves, pero solo tengo un integrador de ejemplo y no encuentro en internet, y no puedo irme hasta Campus…
lo mejor es hacer finales no? son muy parecidos los ejercicios o difieren mucho?
o los integradores juntan un par de ejercicios del primer y segundo parcial?
gracias
Hola Pablo,
Yo te aconsejaría que primero hagas ejercicios de la guía (que podés verificar la respuesta). Después lo ideal para rendir un integrador es hacer parciales ya que es una mezcla de ambos parciales.
Y de última hacé también de finales (aunque son mas complicados porque pueden mezclar temas de la 1º y 2º parte).
En definitiva, hacé todo lo que puedas.
Suerte,
Damián.
Buenas Tardes Damián,
Necesito preparar el final de A2 para mayo y realmente no recuerdo casi nada de la materia.
La curse hace 10 años y ahora deseo retomar la carrera.
Vos das clases particulares para poder prepararla, o podes recomendarme a alguien?
Muchas gracias.
Saludos,
Oscar.
Hola!! Les queria agradecer a Damián y a todos los que participan en este blog ! Hoy aprobe!! Y me sirvió muchisimo esta página!!!
Saludos,
Andrea
hola Damián, cómo resuelvo este ejercicio? Tengo dudas con el planteo de cuál es S o si tengo que hacer dos integrales por separado con Stokes. El enunciado dice así:
Verificar el Teorema de Stokes siendo F(x,y,z)=xz.i+z.y^2.j+a.k y S la superficie x^2+y^2 =z con 1<=z<=4
Mil gracias!
Saludos
Angeles
Hola Angeles,
Primero calculá el flujo del rotor sobre la superfice, yo la parametrizaría como
con
Después, para verificar Stokes, tenés que hacer la circulación del campo sobre la curva frontera, que en este caso está separada en dos partes.
Yo las parametrizaría como
en ambos casos con
Fijate que orienté
en la otra dirección, lo importante es que la orientación de la superficie y la/s curva/s frontera sea consistente (regla de la mano derecha)
Suerte,
Damián.
Hola Damián, estoy tratando de resolver el ejercicio 15 del TP 5 y me quedé media trabada. Me podrás ayudar?
Gracias
Hola Fernanda,
Decime que duda tenés así me fijo como orientarte.
De última la resolución está acá.
Suerte,
Damián.
Hola Damian, prodrias plantear el ej 6 de la unidad 10?
Gracias!
Lo que no estoy entendiendo es porq la circulacion de C1 que me da como dato es 7pi
Hola Sergio,
Es medio complicado de explicar ese ejercicio; el problema principal está en que el dominio no es símplemente conexo como para aplicar Green así nomas.
Si sigue sin salirte acá está la resolución Tp.10 Ej.6
Saludos.
Hola Dami, Quería saber que días esta el curso cuatrimestral de la noche del profesor Carnevali?
Saludos y muchisimas gracias!
Hola Lily,
Tengo entendido que lunes y miércoles.
Suerte.
Damián, quería hacerte la siguiente consulta:
Mirando el ejercicio TP8 EJ6 d) veo que es mucho más facil resolver algunas integrales multiples usando transformadas (no me refiero especificamente a cilindricas o polares)
También encontré ejemplos acá:
http://www.wikimatematica.org/index.php?title=Cambio_de_variables_en_integrales_m%C3%BAltiples
Mi consulta es:
Como me doy cuenta cual es la transformada que me conviene usar?
Veo que en los ejemplos que cito los limites quedan mucho más sencillos, pero no veo la forma de darme cuena yo por mi cuenta cual es la transformada conveniente para cualquier caso.
Hay algún metodo para darse cuenta? O por lo menos alguna forma de probarlo que no lleve tantos calculos?
Gracias!
Hola jicnacho,
Como bién decís, hacer un cambio de variables a veces simplifica mucho la resolución de una integral. (Por ejemplo es mucho más fácil calcular el área que «encierra» una circunferencia en polares que en cartesianas).
Aún así calcular dicha área en cartesianas es posible (casi seguro necesites usar la tabla de integrales, pero sale).
De la misma forma el volumen que encierra una esfera puede calcularse con esféricas (claro), pero también sale bastante fácil con cilíndricas.
A lo que voy es que no hay una metodología, o «receta mágica», que te diga cual sistema de coordenadas usar para tal región de integración dada, porque no existe un único sistema de coordenadas ideal para cada región, me explico?
Como regla general, dentro de las regiones que suelen aparecer en esta materia te diría, si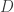
es la región sobre la cual querés integrar, entonces:
Si
y está limitada por rectas, parábolas, o que puedas escribir fácilmente en la forma de fubini 
, 
entonces usá cartesianas.
Si
está limitada por una circunferencia, polares, si tiene simetría respecto de un punto seguro que se usa polares o alguna variante (como desplazarlas, o «estirarlas» para adaptarlas a elipses, creo que me entendés…)
Si
es muy análogo, si tiene simetría respecto de una recta casi seguro cilíndricas. Las más usadas son cartesianas y cilíndricas.
Espero te sirva un poco, como aclaré arriba no es una «receta mágica», pero aún así pensando como es geométricamente la región a veces se puede intuir en que tipo de coordenadas es más fácil trabajar.
Saludos,
Damián.
Gracias Damián por respuesta anterior. En general eso lo tenía claro. Mi pregunta apunta más al caso del ejericio TP8 ej. 6 d)
En ese ejercicio el area encerrada está delimitada por rectas (luego de transformarla tambien) y la transformada no es con coordenadas polares.
Yo me pregunto como (un metodo) encontrar esa transformada tan conveniente para cada caso.
En el ejemplo la transformada es (u+v, u-v). Usarla nos reubica el recinto a integrar con límites muy sencillos y un |J| = 2.
Me gustaría tener una forma genérica de encontrar este tipo de transformaciones (trasnformaciones convenientes para integrar) para cualquier caso.
Gracias
Hola jicnacho,
La mayoría de los métodos de resolución de integrales son heurísticos, si te interesa el tema te suguiero que leas el artículo del algoritmo de Risch que es el que intentan usar los programas como el Maple, Mathematica, etc, para resolver muchas integrales en forma cerrada. (Aclaro que escapa el contenido de esta materia)
Por darte un ejemplo, la función
es contínua y por lo tanto integrable, pero resulta que no tiene una función primitiva elemental, por lo tanto no es fácil expresar la solución de 
de otra forma que no sea símplemente poniendole un nombre a ese número real, o aproximándolo numéricamente 
, o usando funciones no elementales como la función error.
Acá tenés otro ejemplo, si en el Mathematica ponés que te resuelva la integral
te da la aproximación 
, pero cuanto vale exáctamente? (Si existiera un algoritmo para resolver cualquier integral definida, en particular serviría para esta no?)
en la tabla de integrales y avisame que encontrás 😉
Buscá
Si lo querés expresado como un problema de Análisis 2, sería: encuentre el área del recinto
tal que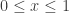 
, 
.
(No importa que transformación hagas, no lo vas a simplificar mucho)
Con respecto al ejercicio que mencionás, la transformación no es necesaria en el sentido de que también se resuelve bastante fácil sin transformar, y no es única, en el sentido de que muchas otras transformaciones también simplifican la resolución de la integral.
No se si respondí tu pregunta, en todo caso si encontrás esa forma genérica de encontrar transformaciones convenientes para integrar («no heurísticamente»), avisame que a mi también me interesa conocerla. 😉
Suerte,
Damián.
Hola Damián,
Yo estoy cursando actualmente con el prof. Bonfante, y quería saber si el 2° parcial es el martes o miércoles próximo, y si sabés cuándo es el recuperatorio del 1°.
Saludos!
espero que sea mañana….
Hola Nicolás,
Hoy miércoles es el 2do parcial del curso de Bonfante.
Saludos.
hola damian,
soy alumno tuyo del curso de los miercoles, te hago una pregunta,
reuelvo un ejercicio por dos formas distintas y no da lo mismo, y en teoria deberia dar, quisas este haciendo algo mal
tengo F(x,y,z)=[x+z^y, x^z -ln(z) , z ]
x^2+y^2+z^2 = 5 z>= 1
div(f) = 5
5 . Int. triple dv
en esfericas =
Int. triple( d∅ ρ^2 senw dρ.dw)
0<Ø< 2π
0< ρ< 2
0< w< Arctg(2)
Øt=14.57 π
ahi deberia dar, pero la resuelvo por cilindricas:
5 . Int. triple dv
5 Int triple dØ ρ dρ dz
0<Ø< 2π
0< ρ< 2
0< z< Sqr[ 5 – ρ^2 ]
eso me da 13.97 π
me podrias dar una mano para saber cual de los dos esta bien planteado, porque no veo el error.
gracias.
saludos
Hola Iván,
que copiastes se tiene que 
así que no se que suponer.
No copiastes el enunciado completo, por lo que tengo que suponer que es lo que querés calcular. Además para la
Supongamos que
y querés el flujo total sobre la frontera del cuerpo 
. Lo hacemos por divergencia.
En ese caso ambas integrales que hicistes están mal porque no se corresponden con dicho cuerpo.
En esféricas es difícil por el plano que aparece. (Además cuidado que donde pusistes
ese no es el ángulo que querés, acordate que debería ser el ángulo desde el eje z, no desde el eje x).
En cilíndricas el error que tenés es que z debe ser mayor a 1 (pusistes cero), y además tenés algún error de cálculo, porque según el wolframalpha la integral que planteastes da aproximádamente 118,371…
Te debería quedar:
según el wolframalpha.
Saludos,
Damián.
perfecto,
si, copie mal el enunciado, a la ultimo es 4z, por eso la div me da 5 ,
y en la carpeta los limites de cilíndricas los tengo como decís,
y el error, esta en el calculo de w. para las esfericas.
gracias damian !!
Hola, quisiera saber cual es la fecha del recuperatorio del 2do parcial, curso con Bonfante los jueves a la mañana en el z2002, o en su defecto el mail del profesor. Gracias y saludos.
Damián, yo curse Análisis Matemático II en el 2008 con el plan viejo (K95) por lo que se me vence este año. Quería consultarte si el final y los temas son los mismos al del K08 (2 teoricos y 4 practicos)
Muchas gracias y te felicito por la página. Es de gran utilidad para estudiar esta materia.
Hola Leandro,
Si, sigue siendo 2 teoricos y 4 practicos. Hay que hacer 1 teórico y 2 prácticos para aprobar.
Saludos,
Damian.
Hola Damián! Yo cursé con vos y con Bonfante este año los días miércoles. Hoy supuestamente era el recuperatorio del 2do parcial, pero se me hizo imposible llegar a la facu por el tema de la lluvia. No hay otra fecha posible para rendirlo?
Muchas garcias.
Hola Pedro,
La información que tengo es la que está publicada acá.
Saludos,
Damián.
hola damian,
rendi el recuperatorio del 2do parcial el jueves pasado con bonfante, en teoria nos dijo que nos mandaba las notas por mail y sino hoy nos la daba en la facultad. pero no aparecio, queria consultarte si tenes un mail para poder comunicarme con el, desde ya muchas gracias
Hola Damián…emepcé a cursar análisis en verano y quería hacerte una consulta sobre la inscripción:Tenés un mail?
Hola Sofía,
Podés preguntarme por acá o sinó el lunes en el aula 37.
Saludos,
Damián.
Hola, quería saber si hay clases de consulta para rendir los finales..
Gracias!
Saludos,
Pamela
Hola,soy David. Queria saber,con respecto a las integrales:Quería Saber en que casos es necesario normalizar el vector normal (hacerlo versor), y en que integrales no es correcto esto?
Y,otra pregunta: Para Stokes,¿el vector normal siempre es saliente,o siempre apunta hacia arriba de la superficie?
Muchas Gracias!Esta muy bueno tu blog!!!!!
David
Hola Soy David, Quería saber como se parametrizan las superficies siguientes que determinan un volumen V. Un plano Z=3(1 + Y/2); un paraboloide Y= 4 -X^2 – Z^2 y un cilindro X^2 + Z^2= 1. Todo esto para aplicar El teorema de la divergencia. Gracias!
Hola Damián, cómo hago para saber la contraseña para ver mi nota del curso de verano?
Muchas gracias
podes hacer alguno eercicios de continuidad por definicion, no le veo el razonamiento
Queria saber, por favor, cuando son los recuperatorios de analisis 2 en febrero/marzo, con el profesor Bonfante, de los dias miercoles a la noche. Muchas gracias.
Me podrian ayudar con este ejercicio:
Y=(2X^3.5)^x
saludos, necesito ayuda con el ejercicio 12 de la guia 6, ya saque la recta tg, para saber si intersecta al cilindro que es lo que tengo que igualar??
Hola Martín,
Ya tenés la ecuación paramétrica de la recta? Es decir la que es de la forma
En ese caso tenés que buscar los valores del parámetr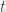o (
o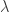 
o como lo llames) que satisfacen la ecuación del cilindro (en este ejercicio el cilindro de ecuación 
).
Es decir buscas los valores de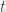
talex que 
. Finalmente reemplazas esos valores de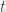 
en la ecuación de la recta y te va dando los puntos de la intersección.
Saludos,
Damián.
loco sos crack, me ayudaste un montón, te dejo dos sugerencias:
1)Fijate de difundirlo más, la verdad lo encontré de casualidad y me vino de 10 este blog. Quizás con más difusión, gente se cope y resuelva más ejercicios y logres tener toda la guía resuelta .
2) fijate de poner los comentarios más actuales arriba, y que el deja un comentario, tambíen se encuentre en la parte superior.
Saludos y gracias por tu aporte desinteresado !!!
Blog absolutamente fenomenal, sinceramente te agradezco muchísimo por tu trabajo, es simplemente espectacular.
Abrazos.
PD: La idea de Lucho sobre los comentarios me parece que vendría muy bien.