Pongo los resultados que daban los ejercicios:
1)
a) La circulación daba 
b) La circulación daba 
2)
b) La circulación pedida daba
3) El volúmen pedido era
4) El área pedida era
Comentarios recientes
Juani Rigada en 2º Parcial Curso de Verano… Santiago Orlando en Final 19/12/2017 damidami en Final 12/12/2017 
Rochas (@agustinroch… en Final 12/12/2017 Emy Goicoechea en Final 12/12/2017 damidami en Final 20/07/2010 Rochas (@agustinroch… en Final 20/07/2010 Rochas (@agustinroch… en Final 19/07/2011 damidami en Final 19/07/2011 Rochas (@agustinroch… en Final 19/07/2011 damidami en Final 21/12/2009 Guido Paolini en Final 21/12/2009 damidami en Tp 3 Ej 3.c Guido Paolini en Tp 3 Ej 3.c Matias Isturiz en Final 24/05/2017 LaTeX
En los comentarios podés escribir expresiones matemáticas usando código
.Por ejemplo si escribís...
$latex 2 \int_0^4 dx \int_0^8 dz = 64 $
...se visualiza como:
Podés practicar en este post.Más información (en inglés)
Análisis Matemático II 
Damian queria preguntarte sobre el 2b, yo lo q hice fue sacar la ecuacion de la linea de campo que me quedo y^2/2 = x/2 + C, donde reemplaze x e y con los puntos q me daban (1,1) y (4,2) y en ambos casos me quedo C = 0 por lo tanto la linea de campo me quedo y = raiz(x) y ahi halle g(t) = (t^2, t) haciendo y= t y luego g'(t) = (2t, 1) y f[g(t)] = (2t^3, t^2) y luego usando nuevamente lo puntos q me daban halle q la integral va desde 1 a 2 de f[g(y)] . g'(t) pero me da 988/15
Queria saber q hice mal y como se resuelve, gracias.
[Te respondió Gonzalo mas abajo. Saludos. – Damián.]
Hola, te hago una pregunta, me recomendas algun libro o si tenes un apunte de lineas equipotenciales, ya que en mi curso no se dio el tema, y me falta ese tema para el final.
gracias.
Hola Sebastián,
Hay muchos temas que están relacionados, y no se bien cual sería tu duda.
Las lineas equipotenciales son simplemente los conjuntos de nivel de la función potencial, es decir son los puntos que satisfacen
Si un campo vectorial admite función potencial se dice que es un campo conservativo.
En cualquier libro de análisis 2 (Ej. Tromba, Stewart, Pita Ruiz) vas a encontrar información sobre la función potencial, que el gradiente es normal a la curva/superficie equipotencial (de nivel k), las condiciones necesarias para que un campo sea conservativo, etc.
Otro tema importante es que las líneas de campo son perpendiculares a las equipotenciales. Este tema que tanto toman en los finales está explicado en el volúmen 3 del Flax, página 436, y la idea básica es usar el hecho de que el gradiente es perpendicular al conjunto de nivel, y tangente a la línea de campo.
También puede servirte la guía teórica de Ecuaciones Diferenciales Ordinarias de la cátedra (BM2AT1) que desarrolla el tema de las líneas de campo.
Espero te sirva de orientación, te dejé algunos enlaces a wikipedia en inglés para ampliar sobre estos temas.
Saludos,
Damián
Hola, probablemente hayas hecho mal las cuentas, acabo de fijarme y el wolfram alpha dice que da 407/15, te adjunto el link del wolfram con la integral resuelta.
link
Saludos.
[Edité el enlace porque aparecía mal en wordpress. – Damián]
Hola que tal, en el 4) me dio parecido pero un poco distinto, las constantes escenciales te quedaban 2/5 y 8/5?
Hola Nicolás,
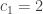y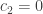 
La solución general me quedaba
Las constantes
Por lo tanto la solución particular era
Saludos,
Damián.
Hola damian, te queria preguntar sobre el ejercisio 3 porque tengo la duda del limite de integracion de titha, porque la proyeccion del volumen q tengo q calcular es una circunferencia de radio 3 con y = 0, pero al decirme y >= x yo a ese circulito lo parti al medio con la recta esa y entonces los limites de titha no me quedan de 0 a 2 phi como habiamos dicho, como es bien este ejercisio?
gracias, un saludo.
Primero hacé el cambio de coordenadas a cilíndricas sobre el eje y, el resto sale fácil. El ángulo es de 0 a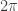
porque en la proyección sobre el plano 
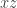queda el círculo entero.
Hola Damian, te queria preguntar del 2b como haces para sacar la ecuacion de la linea de campo. Gracias
Hola Nico,
En general, si tenés un campo vectorial
las lineas de campo las obtenés resolviendo la ecuación diferencial:
En este caso tendrías que resolver
Hola, Damián.
En los ejercicios 1a y b estoy llegando a los mismos resultados pero con el signo cambiado. Estoy usando el mismo vector normal que pusiste vos.
En el 1a, la componente k del rotor del campo me queda «-z». En el 1b, «z-y».
No pude encontrar hasta ahora donde me comí el signo como para que de exactamente al revés.
Saludos,
Hernán
Hola Hernán,
entonces el componente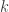 
del rotor viene dado por 
lo cual da 
y no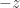 
.
(el vector «nabla» producto vectorial el campo).
Seguro estás calculando mal el rotor.
Si el campo lo denotamos como
Para recordar la fórmula general del rotor podés escribirlo como
El error debe ser del mismo tipo en el 1b.
Saludos,
Damián.
estaba haciendo campo vectorialmente nabla. una gilada.
gracias!
Que tal Damian, acabo de resolver el ejercicio 1-a y me dio 2pi en ves de 20pi. Puede ser que te hayas equivocado o fui yo? Saludos.
Hola Leandro,
que sobre la superficie vale 
. O sea que es constante y sale afuera de la integral, que queda el área de una circunferencia de radio 2 lo cual da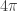 
. Por lo tanto la circulación es 
Los resultados de este final los tengo corroborados con lo que le dió a los profesores y a varios alumnos en la última fecha de final.
Al hacer el rotor producto escalar el versor normal te queda
Aviso que como estoy por salir de viaje, no se si voy a poder responder mas preguntas en lo próximos 5 días. (depende disponibilidad de tiempo y acceso a internet).
Suerte,
Damián.
Damian, como calculaste las constantes en el ejercicio 4). Si lo tenes resuelto estaria bueno que me lo subas asi verifico.
Muchas gracias.
Saludos.
Agustín, no te contesté antes porque estuve de viaje.
Para calcular las constantes tenés que usar el dato de la recta tangente en el punto, y su derivada, te debería quedar un sistema de 2×2 sencillo de resolver.
hola, tengo una consulta, en el ejercicio 3, lo hice con 2 amigos por separado y nos dio a todos 108 pi.
Los limites de integracion fueron, 0<= r <=3, 0<= tita <=2 pi, x<= y <=14-r^2.
Hola,
, no puede aparecer la variable 
en los límites de integración. Por qué reemplazastes a 
para integrar?
Si integrás con las variables
Saludos.
por r cos tita
Es extraño, tenés bien los límites de integración, pero lo revisé y me sigue dando
. Tendrías que poner el desarrollo que hicistes para ver si encontramos un error.
Te cuento como lo hice yo:
La segunda integral da 0 porque
. Seguimos con la primera integral
Viendo esta resolucion que dejo damian me surgio una pequeña duda. En el ejercicio dice Y >= X esto proyectado en el plano xz como se hizo en esta resolucion daria los puntos q x <= 0, por esto seria media circunferencia en vez de una circunferencia entera como en esta resolucion se plantea. y tita variaria de pi/2 a -pi/2 es esto correcto o tengo un error de concepto???
Hola Bruno,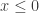
.
No entendí lo de puntos q x <= 0.
Por las dudas fijate que el ejercicio no pide primer octante ni nada parecido, no hay problema que haya
Saludos,
Damián.
Hola damian, en el ejercicio te dan como dato y>=x por lo tanto en el plano xz o y = 0 te quedan los valores de x<0 por lo tanto es media circunferencia como afirma un compañero mas arriba. ya que en el espacio R3 nos queda un cilindro cortado por un plano que es y = x. Por esto tita varia de pi/2 a -pi/2 en mi opinion. Se entendio?. Gracias por responder tan rapido…. mas ahora que estamos en epoca de finales =)
ya lo entendi, Gracias. Saludos ignora el segundo comentario.
Damian, vengo igual que vos resolviendo la integral pero me pierdo cuando haces \int_0^{2\pi} d\phi \int_0^3 14\rho-\rho^3 d\rho – \int_0^{2\pi} \cos(\phi) d\phi \int_0^3 \rho^2 d\rho
No podias sacar el cos(\phi) afuera de la integral esa, es decir: \int_0^{2\pi}cos(\phi) d\phi \int_0^3 14\rho-\rho^3 d\rho – \rho^2 d\rho
No me da haciendolo asi y no entiendo por que.
Saludos
Damian, vengo igual que vos resolviendo la integral pero me pierdo cuando haces
latex \int_0^{2\pi}cos(\phi) d\phi \int_0^3 14\rho-\rho^3 d\rho – \rho^2 d\rho
No me da haciendolo asi y no entiendo por que.
Saludos
Hola Ezequiel Martin,
Escribí tu resolución (si es posible en latex) y vemos porque no nos da lo mismo, sino es muy difícil saber porque.
Saludos,
Damián.
Hola Damian.
Queria preguntarte acerca del calculo de la integral doble en el ejercicio 4.
¿Como te quedan los limites de integracion? porque no me queda claro el calculo (X = 4 y Y=F(X) se intersectan practicamente en el infinito jaja)
Gracias.
Hola Sergio,
, o capaz te estás olvidando de la otra restricción: 
La verdad no tengo a mano la resolución, tendrías que escribir el desarrollo de lo que hicistes para ver si está bien, pero lo que recuerdo es que quedaba una integral sencilla, capaz no te dió bien
Saludos,
Damián.
Damian te quería hacer una consulta del ej 1b) puede ser que del Jacobiano prod. vect del normal se desprende que Q´x-P´y = y – z = y – 9 y de ahi salis a la integral doble, y de esta de queda solo la parte del 9 ya que la otra de 0?
Gracias.
Hola Pablo,
No tengo la resolución a mano. La pregunta no es del todo clara, no indicás que superficie tomás, pero entiendo que tomás un plano y lo que decís parece ser correcto. No me acuerdo si la otra integral daba cero, pero si te dió lo mismo el ejercicio seguro que está bien.
Saludos,
Damián.
Chicos,
Como hicieron el 1.b.) los límites de integración, porque a mi me quedo integral doble de 0 a 2pi y la otra de 0 a 3 de lo siguiente -9, me da -54pi no me da -81pi como aparece en el resultado.
Saludos y muchas gracias a todos!
Me sumo a la inquietud de Lily… a mi me dio -27pi 😦
Pueden poner los limites de integracion y los integrandos a ver en que pifie? Muchas gracias!
Hola JM, y Lily si les sirve, la curva parametrizada es de la forma
los vectores elementales
haciendo
y tomando como límites de integración
obtenes el resultado propuesto por dami
saludos
me olvidada de los vectores elementales haciendo
luego
saludos
Gracias Sergio, un grande!
hola, me estoy preparando para dar el fina. estoy haciendo este final y vi que el ejercicio 2.b respondiste que era con el rotor, pero yo lo hice con la formula de la circulacion, y me da lo mismo, esta bien ?
o siempre que se pueda aplicar alguno de los teoremas hay que apricarlo?
Aplique el rotor porque para mi en este ejercicio en particular me parecia mas sencillo por un tema de cuentas, como se cumplian todas las hipotesis…..No esta mal si lo haces por definicion, te manejas con las herramientas que mejor conozcas, a no ser que en el enunciado te digan explicitamente «use tal teorema»., bueno ahi no te quedaria otra .
gracias!
Buenas.
A mi no me queda claro el 1b) . Damian puso «…considerando el versor de la superficie como n=(0,0,1)…» . Y en la respueta de sergio usa como n el producto vectorial de los vectores elementales. Ambos son correctos? Porque no llego al mismo resutaldo . Gracias
buenas damian, te hago una consulta del 2b. Te piden la circulacion de un punto a otro por lo tanto yo cree una recta lineal que uniera los dos puntos en cuestión, halle una g(t) y calcule la circulacion con la integral de circulacion, ahora bien cuando veo las respuestas habia que hallar la linea de campo, no entiendo porque habia que hacer esto, nose si es algo teorico que me falta o simplemente porque en el item a te pedia sobre las lineas de campo. gracias y saludos.
Hola Rochas,
donde 
.
Te piden la circulación a lo largo de la línea de campo. Como dicho campo no es conservativo, la circulación depende del camino así que no podemos estar seguros que de lo mismo ir por una recta, lo mas probable es que de distinto.
Para hallar la línea de campo resolvé la edo