Preguntas frecuentes

preguntas-frecuentes

En esta página tengo pensado ir agregando las preguntas que surgen con mas frecuencia en este blog de los alumnos que cursan esta materia.

1.) ¿De donde sale el -1 cuando calculamos el vector normal a una superficie como (f'_x, f'_y, -1) ?
Respuesta

2.) Me piden calcular el límite \displaystyle \lim_{(x,y) \to (0,0)} f(x,y). Ya probé por rectas de la forma y=mx y por parábolas de la forma y = kx^2 y sobre todas las curvas el límite da 0. ¿Eso significa que el límite existe y vale cero?
Respuesta

3.) ¿No faltó agregar el \rho del jacobiano?
Respuesta

4.) Estoy calculando una integral de circulación/flujo, ¿adentro de la integral va el vector o el versor tangente/normal?
Respuesta

5.) Estoy resolviendo un ejercicio de integrales y me queda para calcular el área que encierra una circunferencia o elipse, o el volúmen de una esfera… ¿Puedo usar la fórmula conocida en lugar de resolver la integral?
Respuesta

6.) ¿Qué bibliografía recomendás para complementar la materia?

Respuesta

7.) ¿Sabés cuando toma recuperatorios el profesor x? ¿Cuando hay clases de consulta? ¿Le podés preguntar al profesor y que me saqué? ¿Me darías el email o teléfono del profesor z?
Respuesta

8.) ¿Porqué tardan en subir la resolución del final \pi? No me sale ninguno de esta lista de 42 ejercicios.
Respuesta

9.) Tengo f(x,y) = ( y + y\phi(xy), 2x + x\phi(xy)). Cuando calculo Q'_x - P'_y me queda
2 + \phi(xy) + xy\phi'_x(xy) - [ 1 + \phi(xy) + yx\phi'_y(xy) ] = 1 + xy (\phi'_x(xy) - \phi'_y(xy)) .
Socorro, no se cancelan las derivadas parciales, ¿que estoy haciendo mal?
Respuesta

10.) ¿Das clases particulares, o podés recomendarme a alguien que lo haga?
Respuesta

1.) ¿De donde sale el -1 cuando calculamos el vector normal a una superficie como (f'_x, f'_y, -1) ?

Hay varias formas de explicar esto. Cuando tenemos una función diferenciable f:D\subseteq \mathbb{R}^2 \to \mathbb{R} (digamos z=f(x,y)) decimos que la gráfica de la función, o sea los puntos de la forma (x,y,f(x,y)), define una superficie.

El vector normal entonces lo calculamos de la forma usual (suponiendo que la superficie es regular), definiendo la función F:D\subseteq \mathbb{R}^2 \to \mathbb{R}^3 tal que F(x,y) = (x,y,f(x,y)) (notar que no es lo mismo F que f), calculamos el vector normal como
n = F'_x \wedge F'_y = \left| \begin{matrix} i & j & k \\ 1 & 0 & f'_x \\ 0 & 1 & f'_y \end{matrix} \right| = (-f'_x, -f'_y, 1)

Y si n es un vector normal entonces N=-n también lo es, es decir N=(f'_x, f'_y, -1)

Otra forma de calcularlo es usando el hecho de que el gradiente es normal al conjunto de nivel, entonces definiendo G(x,y,z) = f(x,y)-z tenemos que el conjunto de nivel 0 de G equivale a la gráfica de la función original f(x,y), por lo tanto
G(x,y,z) = f(x,y) - z
\nabla G(x,y,z) = (f'_x, f'_y, -1)

donde denuevo vemos que aparece el -1 «mágico». 😛

Un error común es pensar que el gradiente es normal a «todo» lo que respecta a una función f(x,y), y por lo tanto querer calcular el vector normal a la gráfica de la función como \nabla f(x,y) = (f'_x, f'_y), pero observemos que este nunca puede ser el vector normal a una superficie, puesto que debería ser un vector de \mathbb{R}^3 pero tiene solo 2 componentes! 😯

2.) Me piden calcular el límite \displaystyle \lim_{(x,y) \to (0,0)} f(x,y). Ya probé por rectas de la forma y=mx y por parábolas de la forma y = kx^2 y sobre todas las curvas el límite da 0. ¿Eso significa que el límite existe y vale cero?

Respuesta corta: NO.

Respuesta larga: Probar que el límite existe por algunas curvas no implica que el límite exista en general. Incluso aunque se prueben infinitas curvas, como las familias infinitas de rectas y parábolas de la pregunta, porque siempre puede haber OTRA curva por la cual el límite podría llegar a dar distinto, por ejemplo a lo mejor aproximándose por la curva de ecuación y= \sin(x) el límite de 1 y no cero, y por lo tanto en ese caso el límite no existiría.
¿Y entonces como pruebo que existe un límite? Si el límite realmente existe, para probarlo usualmente usamos el método «infinitésimo por acotado» (por ejemplo para f(x,y) = x \sin(y) ), aunque otro método que funciona a veces es hacer un cambio a una variable (por ejemplo para f(x,y) = \frac{\sin(x^2+y^2)}{x^2+y^2} haciendo t=x^2+y^2).
En todos los casos los límites los resolvemos usando propiedades de límites; la definición de límite sólo nos interesa a nivel teórico, no práctico.

3.) Supongamos que me piden calcular el área de la superficie \Sigma de ecuación z^2 = x^2 + y^2 con 0 \leq z \leq 1.

Y entonces parametrizo la superficie con
g : D \subseteq \mathbb{R}^2 \to \mathbb{R}^3
tal que g(\rho, \phi) = (\rho \cos(\phi), \rho \sin(\phi), \rho)
con D = \{(\rho,\phi) \in \mathbb{R}^2 : 0 \leq \phi \leq 2\pi, 0 \leq \rho \leq 1 \}.
Entonces,
g'_{\rho} = (\cos(\phi), \sin(\phi), 1)
g'_{\phi} = (-\rho \sin(\phi), \rho \cos(\phi), 0)
g'_{\rho} \wedge g'_{\phi} = (-\rho \cos(\phi), -\rho \sin(\phi), \rho)
|| g'_{\rho} \wedge g'_{\phi} || = \sqrt{ \rho^2 + \rho^2} = \sqrt{2} \rho
Y finalmente
Area(\Sigma) = \int_0^{2\pi} d\phi \int_0^{1} \underbrace{\sqrt{2} \rho}_{||g'_{\rho} \wedge g'_{\phi}||} d\rho = \sqrt{2} \frac{1}{2} 2\pi = \sqrt{2} \pi

La pregunta es: ¿No faltó agregar el \rho del jacobiano?

Respuesta corta: No.

Respuesta larga: Por la forma en que se resolvió el ejercicio (la forma en que se parametrizó la superficie), no hizo falta hacer ningún cambio de variables. El jacobiano se agrega cuando se aplica el teorema de cambio de variables, y al resolverlo de esta manera no fue necesario. Diréctamente parametrizé la superficie «basandome en las coordenadas polares» (que no es lo mismo).

4.) Estoy calculando una integral de circulación/flujo, ¿adentro de la integral va el vector o el versor tangente/normal?

Hay dos formas de interpretar las integrales de circulación y de flujo: la clave está en como interpretamos el diferencial (de curva o de superficie respectivamente). Explico para el caso de superficie y flujo, pero se entiende que el caso de curva y circulación es análogo. Sabemos que la integral de un campo escalar f : D \subseteq \mathbb{R}^3 \to \mathbb{R} sobre una superficie S \subseteq D se denota \iint_S f dS y se calcula como \iint_D f(g(u,v)) ||g'_u \times g'_v|| dudv, podemos decir que el diferencial de superficie (escalar) corresponde a dS = || g'_u \times g'_v || dudv. Hasta acá ni hablamos de vector ni versor normal (porque no hace falta).
Cuando lo que queremos integrar es un campo vectorial f : D \subseteq \mathbb{R}^3 \to \mathbb{R}^3 (es decir queremos calcular el flujo de f sobre S), importa la orientación de la superficie, y por lo tanto la dirección de un vector (o versor) normal a la superficie. Podemos definir el flujo utilizando el versor normal de la siguiente forma:
\iint_S f \cdot n dS = \iint_D f(g(u,v)) \cdot n || g'_u \times g'_v ||dudv
donde n es un versor normal, el que viene dado por:
n = \frac{g'_u \times g'_v}{|| g'_u \times g'_v||}
Si prestás atención, la norma aparece en el numerador y el denominador así que se cancela, y lo que queda es
\iint_D f(g(u,v)) \cdot (g'_u \times g'_v) dudv
Por esta razón es que algunos definen un diferencial de superficie vectorial como
dS = (g'_u \times g'_v) dudv
y definen la integral de superficie como
\iint_S f \cdot dS = \iint_D f(g(u,v)) \cdot (g'_u \times g'_v) dudv
es decir sin utilizar ningún versor normal, sinó utilizando el vector normal g'_u \times g'_v que no necesariamente es versor.
Las dos formas son correctas y llevan al mismo resultado, pero esta última es la forma que yo utilizo personalmente, por considerarla mas prolija conceptualmente, y para no andar tachando todo el tiempo dichas normas que de todas formas se cancelan (y ni siquiera es necesario calcularlas).

5.) Estoy resolviendo un ejercicio de integrales y me queda para calcular el área que encierra una circunferencia o elipse, o el volúmen de una esfera… ¿Puedo usar la fórmula conocida en lugar de resolver la integral?

Respuesta corta: Si.

Respuesta larga: Si el enunciado no pide explícitamente que uses integrales, no hace falta hacerlo. Estríctamente hablando, puede que a algún profesor no le guste el hecho de que no resuelvas la integral a mano, en caso de duda preguntale a tu profesor que le parece, o a algún profesor de la mesa de examen si estás dando el final.

Yo lo hablé con varios profesores, y todos estaban de acuerdo en que se acepta. Uno me contestó que en jurisprudencia existe el in dubio pro reo, que significa que en caso de duda se beneficia al acusado 😉

Si un profesor quiere evaluar que sepan integrar, no va a poner un ejercicio donde quede una región reconocida para calcular su área/volúmen. De última, si no estás seguro y no querés preguntar siempre podés hacer la integral que en esos casos nunca es muy difícil, es mas bien una cuenta molesta que te ahorrás de la otra forma.

6.) ¿Qué bibliografía recomendás para complementar la materia?

Respuesta corta: El Marsden-Tromba, Stewart, Pita Ruiz y Apostol son todos libros buenos que pueden te pueden servir.

bibliografia

Respuesta larga: Primero copio la bibliografía sugerida por la cátedra:

Bibliografía sugerida:
· Calculus Vol 1 y 2 2° edición (unidades temáticas I a X)
Tom M. Apostol, Ed. Reverté S.A.
· Cálculo Vectorial 1° edición (unidades temáticas I a IX)
Claudio Pita Ruiz, Ed. Prentice-Hall Hispanoamericana S.A.
Bibliografía complementaria:
· Cálculo con Geometría Analítica 6° edición (unidades temáticas I a X)
Edwin J. Purcell, Dale Varberg; Ed. Prentice-Hall Hispanoamericana S.A.
· Cálculo Vectorial I 4° edición (unidades temáticas I a IX)
Jerrold E. Mardsen – Anthony J. Tromba, Ed. Addison Wesley Longman.
· El Cálculo 7° edición (unidades temáticas I a IX)
Louis Leithold, Oxford University Press.
· Matemáticas Avanzadas para Ingeniería Vol. I 3° edición (unidades temáticas VI a X)
Erwin Kreyszig, Ed. Limusa Wiley.
· Vectores y Tensores con sus aplicaciones 14° edición (unidades temáticas VI a IX)
Luis A. Santaló, Editorial Universitaria de Buenos Aires.
Bibliografía de referencia para aplicaciones computacionales:
· Mathematica (Domine al Mathematica 99%)
E. Castillo – A.Iglesias – J.M. Gutierrez – E. Alvarez – A. Cobo, Ed. Paraninfo.
· The Mathematica Book
Stephen Wolfram, Cambridge University Press.

Mi opinión personal:  Con la carpeta debería alcanzar para cubrir tanto la teoría como la práctica del programa de la materia, por la que en principio la bibliografía es opcional.  Aclaro esto porque a veces la notación de un libro es distinta a la de un profesor, u otros autores, y puede llevar bastante tiempo intentar «traducir» lo que dice un libro a lo que dice otro.

Ejemplo:

  • Lo que algunos llaman entorno, otros lo llaman vecindad.
  • Lo que a algunos llaman suave otros llaman diferenciable, pero para otros es sinónimo de infinítamente diferenciable.  Para algunos es una propiedad de las funciones, pero para otros lo es de conjuntos como curvas o superficies.
  • Lo que algunos llaman curva, otros lo llaman trayectoria.
  • Etc.

Aclarado ese asunto, comento mi opinión personal (al día de hoy) respecto de algunos libros de la bibliografía.

Pita Ruiz.  Ventajas: Es uno de los más claros y completo, uno de los más recomendables.  Desarrolla los conceptos intuitivamente y va construyendo los conceptos más abstractos de a poco partiendo de casos más concretos, tiene muchos ejemplos e ilustraciones.  Desventajas:  Es el más extenso (1077 hojas), lo cual hace que no sea muy portable, y que cada tema lleve bastante tiempo de leer.  No tiene ecuaciones diferenciables.  Conclusión:  Uno de los mejores para seguir la materia, pero no para leer el último día antes del final.

Calculus 2 de Apostol. Ventajas: Es la «biblia» del cálculo vectorial, demuestra todos los teoremas y excede el contenido de esta materia (incluye cosas de algebra lineal y probabilidades).  Desventajas: Si bien incluye ejemplos e ilustraciones, tal vez no sea el libro más didáctico para el que recién está viendo los temas por primera vez.  Conclusión:  Excelente como material de consulta ante alguna duda con algún teorema o alguna definición. Y para estudiantes que quieran profundizar sus conocimientos teóricos de la materia.

Cálculo Multivariable de Stewart.  Ventajas: Los conceptos los desarrolla cláramente y con varios ejemplos y ilustraciones muy coloridas, es bastante agradable de leer. Desventajas: Tal vez se queda corto con algunos temas, por ejemplo no menciona la regla matricial de derivación compuesta, ni la matriz hessiana para cálculo de extremos.  Conclusión: Un muy buen libro para complementar la carpeta.

Cálculo Vectorial de Marsden y Tromba.  Ventajas: Muy buena combinación de explicación clara y rigurosa, con ejemplos y demostraciones.  Desventajas:  No tiene ecuaciones diferenciales.  Conclusión:  Uno de los mejores libros para complementar la materia.

Análisis Matemático II de Rafael Flax.  (Aunque no está en la bibliografía oficial, lo menciono porque es muy popular y sé que muchos lo utilizan).  (Son 3 tomos en total).  Ventajas:  Está escrito por un ex-profesor de la UTN, y enfocado en la resolución de ejercicios de finales. Desventajas:   Sólo demuestra los teoremas que se les exige saber demostrar.  Las integrales de superficie (2do tomo) las resuelve de una forma distinta a mi preferencia personal (yo prefiero el enfoque paramétrico). Conclusión: Como el mismo Flax menciona en la introducción, el libro no pretende sustituir la teoría de los otros libros de textos.  Sirve para ganar una idea rápida de que se toma y como se resuelven los ejercicios de exámenes.

Wikipedia.  (no es un libro pero quiero mencionarlo).  Ventajas: Es gratis y fácilmente disponible en internet.  Desventajas: Hay que tener cuidado porque puede llegar a contener algún que otro error.  Conclusión:  No es un libro, pero puede servir para reforzar conceptos.  La wikipedia en inglés está mucho más completa que en castellano.

Hay muchos libros más que pueden ser útiles para complementar la materia, no puedo mencionarlos todos, está en cada uno sacar de cada libro lo que le pueda servir.  De todas formas, como dije al principio, considero que la bibliografía es opcional si se tiene una carpeta completa.

7.) ¿Sabés cuando toma recuperatorios el profesor x? ¿Cuando hay clases de consulta? ¿Le podés preguntar al profesor y que me saqué? ¿Me darías el email o teléfono del profesor z?

Respuesta corta: No se, no puedo preguntarle, y no puedo darte el email ni teléfono de ningún profesor. Este no es el lugar para estas preguntas.

Respuesta larga: Este no es un blog oficial de la cátedra. Es un blog personal cuya finalidad es ser útil a quienes están estudiando la materia Analisis Matemático II.

No soy un intermediario entre alumnos y profesores. Ni un administrativo que puede averiguarles las fechas de tal o cual exámen. Cada profesor es responsable de hacerle saber a sus alumnos toda la información que necesitan en su curso y de poder comunicarles lo que crean necesario. Y sus alumnos son responsables de estar presentes en el momento y lugar en que dicha información les es comunicada.

No tengo el contacto de todos los profesores. Ni es mi responsabilidad preguntarles sobre fechas ni alumnos. Además, no me quiero arriesgar a que me digan una fecha, publicarla, que la cambien y después me digan que yo dije cualquier cosa.

A lo mejor se o sospecho cuando puede ser y puedo decirles eso, o a lo mejor no. Si se o sospecho algo lo comento (pero no es mi responsabilidad que esa información sea correcta).

Ese tipo de cosas las deberían consultar diréctamente a su profesor, y de no ser posible a lo mejor los puedan ayudar en bedelía o en el departamento de matemáticas.

Dejo un enlace a la página del departamento de matemática: http://www.carreras.frba.utn.edu.ar/matematica/

8.) ¿Porqué tardan en subir la resolución del final \pi? No me sale ninguno de esta lista de 42 ejercicios.

Respuesta corta: No puedo resolver tu final ni los 42 ejercicios.

Respuesta larga: Con respecto a porqué no «resuelven» un final o ejercicio en particular, simplemente porque no tuve tiempo o ganas o lo intenté y no me salió o no estoy seguro (que se yo). Aclaro que nadie me paga por mantener este blog ni responder dudas por este medio.
Siempre puede cualquiera que tenga ganas resolver el final o ejercicio en cuestión y publicarlo como un comentario en el blog. O compartir sus respuestas para chequear con otros si les da lo mismo.

Esta es una lista de características deseables que tienen las preguntas que más probablemente reciban una pronta respuesta de mi parte:

  1. Son dudas específicas de un sólo ejercicio, o un sólo concepto teórico.
  2. Está copiado correctamente todo el enunciado (prefiero eso a que me digan el ejercicio 8 del tp4, a lo mejor no tengo la guía de tp a mano)
  3. Prefiero que me digan ejercicio 8 del tp4 a un enunciado mal copiado.
  4. Está copiada la parte de la resolución que supieron hacer y no saben como terminar o no están seguros si está bien (prefiero eso a que simplemente me digan que no les salió ese ejercicio)
  5. Usan \LaTeX correctamente.
  6. No requiere de mi parte hacer cuentas largas (como multiplicar matrices o hacer determinantes, o revisar un manejo algebraico largo como la resolución de una integral que andá a saber donde está el error). Si tienen suerte a lo mejor me pongo a hacerlo pero estas preguntas tardan más en responderse.

9.) Tengo f(x,y) = ( y + y\phi(xy), 2x + x\phi(xy)). Cuando calculo Q'_x - P'_y me queda
2 + \phi(xy) + xy\phi'_x(xy) - [ 1 + \phi(xy) + yx\phi'_y(xy) ] = 1 + xy (\phi'_x(xy) - \phi'_y(xy)) . Socorro, no se cancelan las derivadas parciales, ¿que estoy haciendo mal?

Estas derivando mal. La función \phi no depende ni de x ni de y, por eso no tiene sentido hacer \phi'_x ni \phi'_y. Depende de otra variable, que podemos llamar t. Lo que ves que depende de (x,y) en realidad es la compuesta \phi(xy) = h(x,y).
Cuando derivo la compuesta, debo usar la regla de la cadena, por ejemplo h'_x(x,y) = \phi'(xy)y

Luego debería quedar así
Q'_y - P'_y = 2 + \phi(xy) + xy\phi'(xy) - [ 1 + \phi(xy) + yx\phi'(xy) ] = 1

10.) ¿Das clases particulares, o podés recomendarme a alguien que lo haga?

No doy clases particulares, ni puedo recomendar a nadie que lo haga. Siendo profesor de la facultad no corresponde.

Lo que si les puedo recomendar son las clases de consulta que ofrece la utn. Suelen ser una vez por semana, tienen que averiguar el día y horario, que suelen ponerlo en las carteleras de la entrada, o enfrente de bedelía.

Suelen ir pocos alumnos así que son casi particulares, casi nunca se usa el pizarrón sino que se responden dudas individualmente, o al menos así fueron aquellas en las que estuve presente.

18 respuestas a Preguntas frecuentes

  1. sergio dijo:
    agosto 8, 2011 en 6:20 am

    Hola espero me podas colaborar tengo este enunciado

    Hola tengo el siguiente enunciado

    calcule el flujo de f(x,y,z)=(x^2z^2,1+xyz^2,1-xz^3) a travéz de la superficie de ecuación y=x^2+z^2 con y0

    reemplazando en

    \displaystyle\iint_S f\hat{n}ds=\displaystyle\iiint_V div(f)dV-\displaystyle\iint_{S_1} f\hat{n}dS_1=0-4\pi=-4\pi

    sin embargo la respuesta es 4\pi :banghead:, ahora si tomo (0,-1,0) llego perfectamente al resultado pero no a la orientación que se

    dá como respuesta, en donde me equivoco? :banghead: :banghead: :banghead:, espero su ayuda y orientación

    saludos

    Responder
  2. sergio dijo:
    agosto 8, 2011 en 6:22 am

    correccion donde dice y0 debe ser y<4

    Responder
  3. sergio dijo:
    septiembre 19, 2011 en 6:59 pm

    Hola dami te quería hacer una pregunta , resolví el final tomado el 28/02/2011 y buscando acá no lo encontre para comparar respuestas, basicamente tengo la siguiente duda con este ejercicio

    1) Enuncie las hipótesis que permitan calcular la derivada
    f'(A,r) de un campo escalar f mediante su gradiente, En estas condiciones calcule f'((3,2,2)(1,2,5)) cuando
    f(x,y,z)=g(2x-y)+z^2 , mi planteo

    f'(A,r)=\nabla f(A)\hat{u}

    \nabla f(\bar{x})=(2g'(2x-y),-g'(2x-y),2z)_{(3,2,2)}=(2g'(5),-g'(5),4)

    créo que hasta ahi voy bien igual me gustaria tu opion al respecto , ahora la duda, el vector
    r=(1,2,5) no es un versor y según la definición debe serlo ¿tengo que hacer versor ese vector? o puedo hacer directamente f'(A,r)=\nabla f(A)\hat{u}=(2g'(5),-g'(5),4)(1,2,5)=20

    desde ya gracias por toda tu ayuda hasta el momento prestada ;D ;D 😉

    Responder
    • dami dijo:
      septiembre 20, 2011 en 4:53 pm

      Podés comparar cuanto le dieron los resultados de ese final a otros acá: Final 28/02/2011

      Fijate que el ejercicio pide derivada respecto de un vector \overline{r}, no de un versor \hat{r}, o sea no derivada direccional, así que no hace falta «versorisar» el vector, de hecho estaría mal si hacés eso.

      Responder
  4. Daniel dijo:
    noviembre 18, 2011 en 5:55 pm

    Soy un alumno del curso Z2022 y queria saber como acceder a las notas del primer parcial,
    Muchas gracias,
    Saludos.

    Responder
  5. Daniel dijo:
    noviembre 18, 2011 en 6:23 pm

    Listo! ya pude acceder,
    otra consulta: cuando es el segundo parcial?,
    Muchas gracias.

    Responder
  6. Juan Romero dijo:
    diciembre 2, 2011 en 12:31 am

    AM2-Utn-Frba
    Estaba haciendo el ejercicio 10-c de la guia 9 de la catedra

    area de x^2 + z^2 <= 2ax and interior de una esfera de radio 2a
    y centro en el origen.

    Lo plantee y veia un un cilindro de radio a y eje x=a
    intersecado con la esfera.
    proyecto sobre el plano xz con polares y me queda
    0< phi < 2 π
    0< rho < a
    -sqrt ( 4*a^2-rho^2 ) < y < sqrt ( 4*a^2-rho^2 )

    trato de resolver la integral triple sin olvidar el modulo del derterminante.
    y me queda una integral complicada de resolver,
    ademas de que no pude llegar al resultado que da la guia que es
    16/9 a^3 (3 π- 4)

    ¿estoy haciendo algo mal?
    ¿existe alguna otra proyeccion o coordenadas que quede mas sencilla la integral?

    Saludos

    Responder
    • dami dijo:
      diciembre 2, 2011 en 10:01 am

      Hola Juan Romero,
      Cuando planteás una integral y querés saber si te da igual que en la guía sin resolverla a mano, podés user el wolframalpha.

      En tu caso lo que veo mal es que al proyectar sobre el plano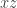 xz la circunferencia no queda centrada en el origen, y vos tomastes polares como si estuviera centrada.

      Intentalo de nuevo, de última ese ejercicio está resuelto acá.

      Suerte,
      Damián

      Responder
  7. Christian dijo:
    octubre 15, 2013 en 11:08 am

    Damian,
    quisiera saber como resolver este ejercicio:
    Representar dominio e indicar expresion del conjunto de discontinuidad de :

    f(x,y)= 1+x**2y si x0, x>y*sqrt(3) , x>-y
    1 cualquier otra relacion xy

    Desde ya muchas gracias,
    Christian

    Responder
    • dami dijo:
      octubre 15, 2013 en 11:54 pm

      Hola Christian,

      Tratá de ser más específico con la pregunta. Lo que pide el enunciado es claro: el conjunto dominio, y el conjunto de discontinuidad, es decir formado por los puntos del dominio donde la función no es contínua.

      Por otro lado, no entiendo la función, tratá de tipearla usando comandos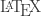 \LaTeX.

      Saludos,
      Damián.

      Responder
  8. Christian dijo:
    octubre 15, 2013 en 11:10 am

    la funcion se publico mal de mi comentario anterior

    f(x,y)= 1+x**2y si x0, x>y*sqrt(3) , x>-y
    1 cualquier otra relacion xy

    muchas gracias,
    Christian

    Responder
  9. luis dijo:
    diciembre 5, 2013 en 7:38 pm

    te puedo consultar por un ejercicio en particular?

    Responder
    • dami dijo:
      diciembre 7, 2013 en 1:45 pm

      Hola Luis,
      Podés preguntar. Intentá copiar todo el enunciado claro y sin errores, y todo el desarrollo que pudistes hacer, y la duda que sea lo más puntual posible.
      Después si tengo tiempo lo miro y te contesto.
      Saludos,
      Damián.

      Responder
  10. Dario dijo:
    May 31, 2014 en 4:14 am

    Hola.
    Tengo dudas en como utilizar la orientación en una integral, cuando debo utilizar Stokes o Gauss (y ya que está también Green).
    Más que nada cuando en el ejercicio dice por ej. «de modo que la normal en el punto (0,0,1) apunte en la dirección (0,1,1)» o cuando dice «con la normal que apunta hacia adentro» o también «en el sentido externo del campo»

    Responder
  11. gonzalo dijo:
    julio 18, 2014 en 9:22 pm

    Hola
    Me gustaria consultar de donde puedo obtener el teorema de schwarz que me permita resolver el T2) del final del 6/8/2013
    Muchas gracias

    Responder
  12. Lucas dijo:
    May 22, 2015 en 1:54 pm

    Damian, como estas? Tengo una preguntita muy breve, cuando me dicen que la densidad en cada punto es proporcional a la distancia desde el punto al plano xy, significa que d=k.|z|^2? Gracias!

    Responder

Deja un comentario