Respuestas:
T1)
T2) 
E1) Salía por circulación directo y daba
E2)
E3)
E4)
Comentarios recientes
Juani Rigada en 2º Parcial Curso de Verano… Santiago Orlando en Final 19/12/2017 damidami en Final 12/12/2017 
Rochas (@agustinroch… en Final 12/12/2017 Emy Goicoechea en Final 12/12/2017 damidami en Final 20/07/2010 Rochas (@agustinroch… en Final 20/07/2010 Rochas (@agustinroch… en Final 19/07/2011 damidami en Final 19/07/2011 Rochas (@agustinroch… en Final 19/07/2011 damidami en Final 21/12/2009 Guido Paolini en Final 21/12/2009 damidami en Tp 3 Ej 3.c Guido Paolini en Tp 3 Ej 3.c Matias Isturiz en Final 24/05/2017 LaTeX
En los comentarios podés escribir expresiones matemáticas usando código
.Por ejemplo si escribís...
$latex 2 \int_0^4 dx \int_0^8 dz = 64 $
...se visualiza como:
Podés practicar en este post.Más información (en inglés)
Buenas! Yo tengo una duda sobre el ejercicio E2. Lo hice por divergencia y el resultado me da 243pi pero negativo. Yo planteé que había que restarle el flujo del plano z=9 al flujo por divergencia. Entonces me queda:
121.5pi-364.5pi
Hola Michelle,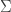
orientada hacia 
.
porque la superficie (el cucurucho) quedó como la tapa “de abajo” del sólido que resulta al poner la tapita plana 
. Intentá visualizarlo, y recordá que la divergencia da flujo saliente.
Está bien lo que hicistes, sólo te falta cambiarle el signo dado que el ejercicio pide el flujo con
Al usar divergencia de ese modo, te quedó orientado hacia
Saludos,
Damián.
Hola damian, con respecto a este ejercicio, se puede plantear directamente la integral triple? Ya que la div f=2, lo que te quedaria 2 veces la integral triple, aplicando coordenadas cilindricas t varia entre 0 y pi/2 el radio entre 0 y 9 y z entre 0 y r…. resolviendolo asi me da directamente 243pi… Es correcto?
Saludos
hola a todos! Alguno que halla visto este final sabe como quedan los limites de integración del punto E3) porque lo intente hacer por coordenadas polares y no si pongo bien entre que varia z.y no me da. Gracias!
cuanto t da? xq a mi me queda entre 0 y 2pi y me da cero 😦
Obviamente esta mal
Después me termino dando. La densidad es δ=k*√(x^2+y^2) como cilindro proyectante te queda x^2+y^2=1 y lo haces por polares : θ entre0 y 2π, ρ entre 0 y1 y z entre (ρ^2 (〖cos〗^2 +3〖sen〗^2 )y (4-ρ^2 (3〖cos〗^2 +〖sen〗^2)
hola. en el E4 como llegan al resultado? Lo que no encuentro es una segunda condición para resolver el PVI (solo llego a la de 5=f(0) ).