
 1ER PARCIAL ANÁLISIS MATEMÁTICO II VERANO 2018
1ER PARCIAL ANÁLISIS MATEMÁTICO II VERANO 2018
Solución: (de la práctica, las demostraciones se vieron en clase)
T1)
a) Nos dan  con
con 
Hay que verificar que 
Derivando parcialmente



Luego


b)  es el Taylor de grado 2 asociado a
es el Taylor de grado 2 asociado a  en
en  .
.

Queremos que 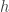 admita extremo local en
admita extremo local en  y clasificarlo.
y clasificarlo.
Como  , entonces
, entonces 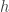 también. Luego los puntos críticos son estacionarios, es decir el gradiente se anula. Como queremos que
también. Luego los puntos críticos son estacionarios, es decir el gradiente se anula. Como queremos que  sea crítico
sea crítico


Del Taylor sabemos que
![f'_x(2,1) = T'_x(2,1) = [ -2 + 8x ]_{(2,1)} = 14](https://s0.wp.com/latex.php?latex=f%27_x%282%2C1%29+%3D+T%27_x%282%2C1%29+%3D+%5B+-2+%2B+8x+%5D_%7B%282%2C1%29%7D+%3D+14&bg=ffffff&fg=333333&s=0&c=20201002)
![f'_y(2,1) = T'_y(2,1) = [ 1 + 2y ]_{(2,1)} = 3](https://s0.wp.com/latex.php?latex=f%27_y%282%2C1%29+%3D+T%27_y%282%2C1%29+%3D+%5B+1+%2B+2y+%5D_%7B%282%2C1%29%7D+%3D+3&bg=ffffff&fg=333333&s=0&c=20201002)
Reemplazando


Es decir debe cumplirse que  , y que
, y que  .
.
Para clasificarlo calculemos el hessiano. Necesitamos las derivadas segundas de 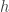 que coinciden con las de
que coinciden con las de  , y podemos obtener del Taylor
, y podemos obtener del Taylor



Luego

por el criterio del hessiano,  es mínimo relativo.
es mínimo relativo.
T2)
b) Dada  , hay que probar que en el punto
, hay que probar que en el punto  resulta
resulta  es perpendicular.
es perpendicular.
Sea  . Entonces
. Entonces  , en particular
, en particular 
Parametrizamos la elipse  con
con  con
con 
Sea ![t_0 \in [0, 2\pi]](https://s0.wp.com/latex.php?latex=t_0+%5Cin+%5B0%2C+2%5Cpi%5D&bg=ffffff&fg=333333&s=0&c=20201002) tal que
tal que  .
.
Sea  . Por ser constante
. Por ser constante  , por otro lado por la regla de la cadena
, por otro lado por la regla de la cadena  . Es decir que
. Es decir que 
Es decir  donde
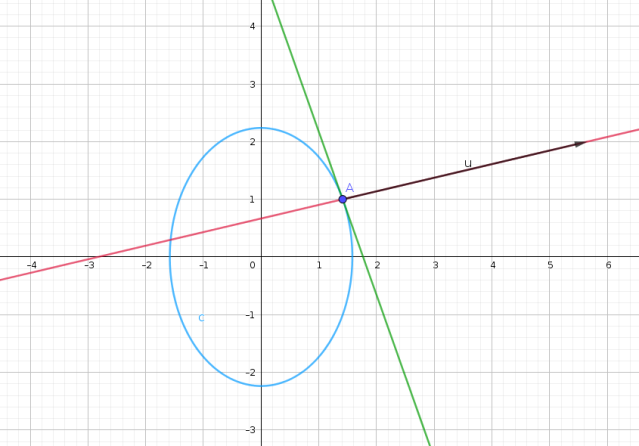
donde  es vector tangente a la elipse. Igual la idea es hacer un dibujito de la elipse y las rectas normal y tangente como sigue.
es vector tangente a la elipse. Igual la idea es hacer un dibujito de la elipse y las rectas normal y tangente como sigue.
La recta normal viene dada por 
La recta tangente viene dada por  tal que
tal que  es decir
es decir  , luego la recta tangente es de ecuación
, luego la recta tangente es de ecuación 
Y el dibujito nos queda así
P1) 
Veamos si es contínua en 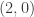 . Debería existir el límite, a ver si es cierto
. Debería existir el límite, a ver si es cierto

Veamos que pasa por la recta de ecuación 

Luego no es continua en 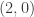 pues el límite debería ser igual a
pues el límite debería ser igual a  . Por lo tanto tampoco es diferenciable en
. Por lo tanto tampoco es diferenciable en 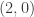
Veamos que onda las derivadas direccionales




La única forma que exista este límite es que  (sino daría
(sino daría  , pero para las derivadas exigimos limites reales).
, pero para las derivadas exigimos limites reales).
Es decir las únicas direcciones en las que es derivable son 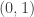 y
y 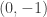 , en donde vale
, en donde vale 
Dibujín de la gráfica de 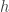

Se ve que algo raro pasa en el punto 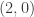 (el eje
(el eje  está en rojo, el eje
está en rojo, el eje  en verde, y el eje
en verde, y el eje  en azul)
en azul)
P2) La parametrización mas directa es considerar la  como un parámetro
como un parámetro  , es decir
, es decir  , con
, con 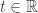 . Cláramente
. Cláramente  (sus coordenadas son polinomios), y además
(sus coordenadas son polinomios), y además  . Esto nos dice que es una parametrización regular.
. Esto nos dice que es una parametrización regular.
Averiguemos 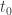 tal que
tal que  . Fácil,
. Fácil,  . Luego
. Luego  es vector tangente a la curva en
es vector tangente a la curva en  . Luego la recta tangente es de ecuación
. Luego la recta tangente es de ecuación

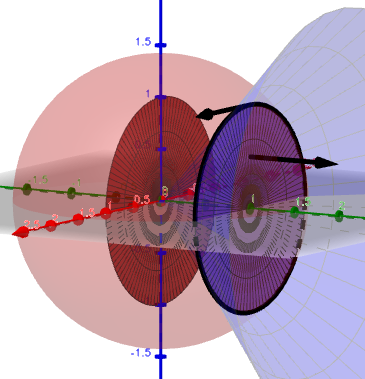
Dibujo todo con el geogebra:
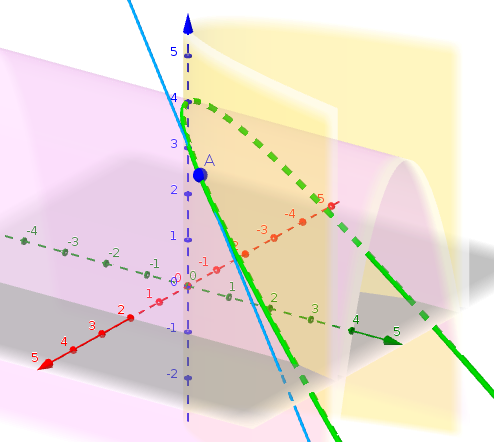
La curva está en verde fluorescente y bien gordita. El punto  está marcado como
está marcado como  . La recta tangente en azul clarito. Y las superficies en amarillo y rosita transparente.
. La recta tangente en azul clarito. Y las superficies en amarillo y rosita transparente.
P3) 
La familia de líneas de nivel (curvas de nivel) viene dada por

busco la familia ortogonal, para eso primero busco la EDO

divido por 2

ok, esa es la EDO. Ahora busco la EDO de la familia ortogonal. Para eso cambio  por
por 

multiplico por 

y ahora la resuelvo para encontrar la familia ortogonal. Primero separo variables



bien, ahí separé variables. Ahora integramos


esa es la familia ortogonal buscada.
Veamos que curvas pasan por el  . De la primer familia obtenemos
. De la primer familia obtenemos  , es decir sólo pasa
, es decir sólo pasa
 (una elipse)
(una elipse)
De la segunda familia obtenemos  , por lo tanto hay una curva y es esta
, por lo tanto hay una curva y es esta
 (una parábola)
(una parábola)
Ahora graficamos todo
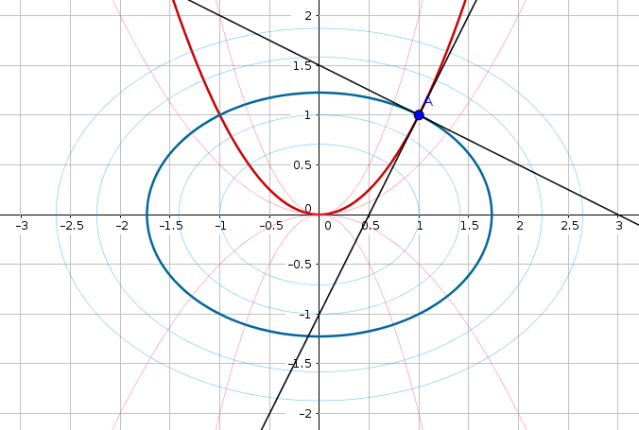
En azul está la elipse, y en rojo la parábola. El punto  se indica como
se indica como  . En negro las rectas tangentes a cada una (que son las normales de la otra respectivamente). Y si uno presta atención, con trazo muy finito hay otras curvas de ambas familias.
. En negro las rectas tangentes a cada una (que son las normales de la otra respectivamente). Y si uno presta atención, con trazo muy finito hay otras curvas de ambas familias.
P4)
a) Nos dan  , con
, con  .
.
De  nos dicen que es
nos dicen que es 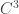 y que el taylor de 2do grado en
y que el taylor de 2do grado en  es
es  .
.
Nos piden una derivada direccional de 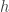 , que es diferenciable por ser composición de diferenciables. Entonces me interesa calcular
, que es diferenciable por ser composición de diferenciables. Entonces me interesa calcular  usando la regla de la cadena. Vemos que
usando la regla de la cadena. Vemos que  . Luego
. Luego



Por otro lado
![f'_u(2,1) = T'_x(2,1) = [ -10x ]_{(2,1)} = -20](https://s0.wp.com/latex.php?latex=f%27_u%282%2C1%29+%3D+T%27_x%282%2C1%29+%3D+%5B+-10x+%5D_%7B%282%2C1%29%7D+%3D+-20&bg=ffffff&fg=333333&s=0&c=20201002)
![f'_v(2,1) = T'_y(2,1) = [ 3 ]_{(2,1)} = 3](https://s0.wp.com/latex.php?latex=f%27_v%282%2C1%29+%3D+T%27_y%282%2C1%29+%3D+%5B+3+%5D_%7B%282%2C1%29%7D+%3D+3&bg=ffffff&fg=333333&s=0&c=20201002)
(Tal vez sería mejor llamar  al taylor para que no haya confusión con los valores de
al taylor para que no haya confusión con los valores de  de
de 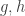 , se entiende que no hay relación.)
, se entiende que no hay relación.)
Luego nos queda


La dirección que va del 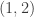 hacia el
hacia el 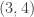 es
es 
Luego la derivada pedida es



b) La función 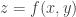 está definida implícitamente por la ecuación
está definida implícitamente por la ecuación  .
.
Hay que determinar la ecuación del plano tangente a la gráfica de  en el punto
en el punto  .
.
Sea 
Verifico que el punto esté en el conjunto de nivel cero.

No hace falta usar Cauchy-Dini, alcanza con usar que el gradiente de  es normal al conjunto de nivel cero de
es normal al conjunto de nivel cero de  en
en  , pues la gráfica de
, pues la gráfica de  coincide con el conjunto de nivel cero de
coincide con el conjunto de nivel cero de  en las cercanias del punto en cuestión.
en las cercanias del punto en cuestión.



Luego un vector normal es 
Otro normal mas lindo por no tener denominadores es  .
.
Luego la ecuación del plano tangente pedido es
![[(x,y,z) - (1,5,3)] \cdot (8,5,-27) = 0](https://s0.wp.com/latex.php?latex=%5B%28x%2Cy%2Cz%29+-+%281%2C5%2C3%29%5D+%5Ccdot+%288%2C5%2C-27%29+%3D+0&bg=ffffff&fg=333333&s=0&c=20201002)





































Debe estar conectado para enviar un comentario.