Pongo los resultados:
T1)
Un vector normal a la superficie en el punto es
La ecuación cartesiana del plano tangente es
E1)
El gradiente de :
El jacobiano de la compuesta:
Parametrización de la recta normal:
Intersecta al plano en el punto
E2)
E3)
E4)
La recta normal queda
Haciendo:
La integral queda:




Damian: ¿como obtengo el vector gradiente de f(3,6)?
Saludos,
Te dan que




Y también que
Sabiendo que
Tenés que
En el mismo ejercicio (E1) como obtenes el punto (9,11,-1) ya que el 9 y el 11 salen del jacobiano pero el -1 de donde? Gracias!!!
Hola Estanislao,
Esa una pregunta muy frecuente y no da explicarla cada vez que la preguntan en el blog, por eso acabo de iniciar una sección de preguntas frecuentes, así que acá esta
la respuesta.
Suerte!
Damian: Como obtengo la recta normal en el punto E4??. El resto del ejercicio me sale pero me trabe en esa parte. Desde ya muchas gracias por tu tiempo.
Hola Matias,



 y un vector tangente a la recta (que es el normal a la curva)
y un vector tangente a la recta (que es el normal a la curva) 
Hay muchas formas, por ejemplo si «pasás a imlícita» la ecuación, es decir considerás la función
su gradiente es normal a la curva de nivel en cada punto
en particular
Ya tenes un punto
con eso deberías poder construir la ecuación vectorial de la recta, la paramétrica, y de ahí pasarla a ecuación cartesiana.
(hay otras formas de llegar a la ecuación sin pasar por la paramétrica, pero esta me parece mas fácil)
Suerte.
damian el punto A me dio q no era regular
perdon me habia copiado mal. estaba hablando del teorico 1
Hola Matías,
Si querés copiá el desarrollo que hicistes así lo revisamos.
Hola, En E3 no es un superficie compacta,conexa sin borde (esfera de radio=2) y la divergencia de F= 3,
donde es mas facil usar el teorema de divergencia?
Hola Alex, desconocida que complica la integral para hacerla directamente.
desconocida que complica la integral para hacerla directamente.
No entiendo del todo tu pregunta. La superficie del E3 si tiene borde, pues no es cerrada al no ser toda la esfera (es solo la parte de arriba), y la divergencia no da 3 sino que da 1.
Conviene divergencia a pesar que hay que restar la tapa porque en el campo aparece una funcion
Saludos.
Si tenes razon z+ por la raiz, y la divergencia le sumaba 2 sin derivar, gracias.
Alex, es difícil entender que estás diciendo. Lo de «z+ por la raíz» entiendo que te referís a que va la parte de arriba de la superficie porque hay una raíz cuadrada. Lo de «y la divergencia le sumaba 2 sin derivar» no tengo idea que es, pero la divergencia da 1 y no se suma sinó que se integra.
Hola, una pregunta.
No entiendo en el punto 3, porque dividen la superficie. El enunciado no se refiere a la tapa superior solamente sino a toda la esfera. No sería directamente Flujo = Int triple de la div?
Como me doy cuenta que no se refiere a toda la esfera?
Si hago el volumen de la esfera, me da 32/3 pi.
Qe estoy haciendo mal?
Muchas gracias!!
Hola Kevin, sale de una raíz cuadrada así que es positivo o cero.
sale de una raíz cuadrada así que es positivo o cero.
No es toda la esfera, es la mitad de arriba. Fijate que
Saludos,
Damián.
Hola. En el EJ 3, cuando calculas el flujo en la tapa, porque multiplicas por -2. No deberia ser por -1? Dado que la divergencia es igual a 1 y tome como sentido del gradiente de la funcion que contiene a la tapa , en el de las z negativas.
Hola Eduardo,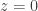 al hacer dicho producto escalar da
al hacer dicho producto escalar da 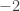 (tomando como decís orientación hacia z negativas)
(tomando como decís orientación hacia z negativas)
No va la divergencia, es calculo de flujo directo, va el producto escalar del flujo por la normal. Sobre el plano
Saludos,
Damián.
Damian, en el ejercicio E3 el grafico de la superficie no seria una esfera? Y por lo tanto seria una superficie cerrada en donde el volumen seria (16/3 pi ) http://s0.wp.com/latex.php?latex=F_%7Btotal%7D+%3D+%5Cleft%28+%5Cfrac%7B4%7D%7B3%7D%5Cpi+2%5E3+%5Cright%29+%5Cfrac%7B1%7D%7B2%7D+%3D+%5Cfrac%7B16%7D%7B3%7D%5Cpi&bg=ffffff&fg=555555&s=0
Desde ya muchas gracias por la respuestas
Saludos , Agustin.
Hola Agustín,
Es lo mismo que preguntó Kevin.
No es toda la esfera es la mitad de arriba.
Saludos,
Damián.
damian, en el ejercicio E3) cuando saco el flujo de la tapa no entiendo por que lo multiplicas por -2, y hago el producto escalar de f con el normal usando las z negativas y me da -2-z, no se en que me estoy equivocando, muchas gracias
javier
Z=0, ya lo entendi, gracias
Damian, no entiendo por que en el ejercicio E4 la integral doble es de «x» dxdy. De donde sale esa X?
Hola Ezequiel,
Le enchufé esa x para despues poder reemplazar en la integral del renglon de abajo.
Saludos,
Damian.
Damián, en los ejercicios del tipo del E3), como te das cuenta la dirección del vector normal? Es decir, el de la tapa, como sabes que va en z negativo?
Gracias!
Hola Tomas,
Orienté la tapa hacia z negativos para que la orientación resulte saliente al sólido, pues usé el teorema de la divergencia.
Saludos,
Damián.
buenas, en el ejercicio 3 el flujo total me esta dando 4, 87 aprox, la divergencia es 1 como dice el resultado y los limites son: en z entra por z=0 y sale por la tapa de arriba (ecuacion dato del ejercicio), resuelvo primero la integral que depende de Z y me queda dentro la ecuacion del limite superior, en funcion de X e Y. Luego se aplica un cambio a polares tomando x como ro por cos(ang) e y como ro por sen(ang), es decir se proyecta sobre el plano XY, pero dentro teniamos la ecuacion de la tapa por lo que queda (raiz de ro al cuadrado + 2) por RO que es el determinante del jacobiano, los limites son de 0 a 2pi el angulo y de 0 a 2 RO, y esa integral doble daria 4.87
Hola Rochas,
El techo quedaría
O sea el flujo total seria

aaaa ya encontre mi error, muchisimas gracias. saludos