Agrego la solución del ejercicio E1.
E1) El campo es
La ecuación de la superficie es
Defino .
Luego el vector normal, con la orientación pedida me queda
Proyecto sobre el plano , me queda un triángulo
.
Luego el flujo pedido es
Agrego la solución del ejercicio E1.
E1) El campo es
La ecuación de la superficie es
Defino .
Luego el vector normal, con la orientación pedida me queda
Proyecto sobre el plano , me queda un triángulo
.
Luego el flujo pedido es
| Juani Rigada en 2º Parcial Curso de Verano… | |
| Santiago Orlando en Final 19/12/2017 | |
| damidami en Final 12/12/2017 | |
| Rochas (@agustinroch… en Final 12/12/2017 | |
| Emy Goicoechea en Final 12/12/2017 | |
| damidami en Final 20/07/2010 | |
| Rochas (@agustinroch… en Final 20/07/2010 | |
| Rochas (@agustinroch… en Final 19/07/2011 | |
| damidami en Final 19/07/2011 | |
| Rochas (@agustinroch… en Final 19/07/2011 | |
| damidami en Final 21/12/2009 | |
| Guido Paolini en Final 21/12/2009 | |
| damidami en Tp 3 Ej 3.c | |
| Guido Paolini en Tp 3 Ej 3.c | |
| Matias Isturiz en Final 24/05/2017 |
En los comentarios podés escribir expresiones matemáticas usando código ![]() .
.
Por ejemplo si escribís...
$latex 2 \int_0^4 dx \int_0^8 dz = 64 $
...se visualiza como:
Más información (en inglés)


Damian,
una pregunta. Como se resuelve el E2? Y la ED del E3?
tendras los resultados?
Muchas gracias por el blog! Es de gran ayuda!
Me sumo al pedido del E2.
Lo que haría seria tomar una recta que pase por f(1)=3. Ej: y=x+2.
Y reemplazaria en H(x,y), es decir: H(x,y)=x.y.(y-x+2) => H(xy)=x.y.y – x.x.y + 2xy. Ahi obtengo la recta tg que en el punto (1,2). Esta bien ? o estoy tirando cualquiera?
En lo que pienso que me equivoco es en tomar una recta cualquiera que pasa por ese punto.
Creo tener una idea. El primer termino de la aproximación es h(1;2) = (1)(2)(f(1))
pero f(1)=3 asi que h(1;2)=6, luego hay que hacer las derivadas parciales de h.
Y acá es una derivada de un producto (el primer factor es otro producto). Pero sobre esta parte no estoy 100% seguro.
Saludos
en el e1 como les quedaron los limites de integracion? a mi me quedo
tita entre 0 y 2pi, ro entre 0 y 4 sen tita y z entre 4-y y xcuad + y cuad -4y
saludos
en el E2)solo hay que hacer regla de la cadena , f es una funcion de una variable sabemos que
por definicion
luego derivamos h de manera convencional, por regla del producto
luego
finalmente
se puede verificar evaluando directamente en la funcion original [hr]
La ecuacion diferencial del E3 la resolves por coeficientes indeterminados o simplemente haciendo el cambio
por coeficientes inderminados, 0 es raiz doble entonces
para la yp, propongo
derivando y haciendo las cuentas respectivas m=-1
luego
tenes las condiciones para determinar a y b…
fe de erratas donde se deriva por regla de la cadena respecto de cada variable en el E2) debe decir
consulta porque la derivada de f(1) te da 1 ? de donde lo sacaste? gracias!
Ah, claro, seria h(xy)=x.y.3. h’x=y3 . h’y=x.3
Entonces le recta tg seria:
z=6 + 6(x-1) + 3(y-2)
y ahi en x e y pones los valores: (1.02;2.02) y obtenes el aproximado
AL FIN PUEDO DECIR: ¡GRACIAS FORO!
Gracias Damián, hace 3 años cursé esta materia y recién este verano me preparé para darla. Sin la ayuda de este blog, imposible habría sido. Gracias nuevamente!
Recuerdo que el T2 había que plantear la divergencia igualado al volúmen de la esfera (4/3 pi r^3) se demostraba que era seis veces el volúmen.
El E1 era la superficie x^2 + (y-2)^2 = 4 con el plano z>4-y. La integral te quedaba de 0:tita:2pi, de 0:r:2 y de 4-y: z :4 y luego la función por la normal (2x,2y-2,0)/2x
El E4, integral de 0 a 2pi, r de 0 a 2, z de 8 a raiz(8-r^2).
Creo que era algo así, saludos y gracias nuevamente!
me parece que el E1, los limites que propones no son. El cilindro esta corrido
saludos
T1) tomo la curva
derivando
el punto dado es regular , se puede agregar que la curva es suave
T2) como bien dicen
E1)
Se puede aplicar el teorema de la divergencia no piden el flujo a traves de
con
div f=3 entonces si aplico una integral doble para el calculo del volumen
para lo limites puedo aplicar polares sobre el recinto
E2) de los datos del enunciado f(1)=3
luego
haciendo las cuentas se cancelan las f'(1), entonces
luego
E3) como bien dicen la solucion de la ED es
de las condiciones
y(0)=2
y'(0)=2
se obtiene que c=b=2 entonces
luego el area estara definida por
E4)
en cilindricas la integral a resolver es
Dami podes arreglar el E4 por favor el limite en z ,
y el limite en tita por fa no me di cuenta antes de subir la respuesta
por error de transcripcion , en el E1 es
por ende el limite en r es
y el flujo sera
avisen si hay otro error mas porfi
con respecto a E3 :
la curva no responderia a : Y = -X^2 + 2 ?
la ed. responde a :
Y= -x^2 + CX + B
Y(0) = 2 = B ( de la condicion 1 )
y con respecto a la segunda, no seria asi :
ec. de recta tg en un punto :
(x,y)= Y'(0)*A + pto
f(x) = ( x, -x^2 + CX + 2 )
f'(x) = (1, -2x + C )
f'(0) = (1, C )
en la ec de la rta tg:
(x,Y) = (1,C)A + (0,2)
X= A
Y = CA + 2
por lo tanto :
Y= CX + 2
para que responda a Y = 2
CX + 2 = 2
por lo tanto C = 0.
quedando
Y = -X^2 + 2
o hay algo mal ?
hola mauricio… si me confundi yo .. la ecuacion que vos propones es la correcta , yo tome como Slatex y'(0)=2 $ y bueno ahi arraste error, lo correcto es y se obtiene la curva que vos indicas
y se obtiene la curva que vos indicas
Hola, me parece que te olvidaste que es un el primer cuadrante. Saludos!
che pero una consulta, el E1 lo hice y me dio 16pi asi como dicen que es con la divergencia. Pero el teorema de la divergencia no dice que tienen que ser SUPERFICIES CERRADAS?
gracias por la ayuda che, de verdad que se agradece muchisimo este blog y toda la ayuda. Saludos
La superficie esta limitada al primer octante y ademas como es la parte sombreada tambien esta limitada por
me define un solido , puedo aplicar divergencia
es
z menor o igual que 4
claro pero fijate que eso en el enunciado nunca lo aclara, de que es z menor o igual que 4, solo te dice que la superficie es en el primer octante y que contiene a esos dos puntos, lo de que es cerrada y llega hasta z=4 es interpretación propia…
A mi me dio 32pi , usando el teorema de la div. ( coinsidero que es cerrado por todas las restricciones );
– desplazaste el cilindro cuando lo pasaste a coordenadas polares ?
x= r.cosq
y=2.r.cosq
con 0<= r <= 2
0<= q <= pi
pero esas coordenadas no son polares, son elipticas, las polares son
no desplaze el cilindro, ademas si vos tampoco lo desplazaste, suponiendo que hayas cometido un error de tipeo en las polares, tenes mal el limite en r
Entiendo lo mismo que Fabi, eh. Sin ánimos de criticar.
no es ninguna interpretacion propia, como bien decis el plano esta limitado por el plano y+z>=4 y llega hasta el plano z=4 pero para poder formar la region sombreada entonces tiene que ser z<=4 , solo estoy planteando lo que veo en el dibujo nada mas, ademas de estar en limitado en el primer octante con todo eso tengo un solido maciso al cual puedo aplicar divergencia …
Toda critica es bien recibida ramiro , no me ofende para nada, al contrario 🙂
Yo tambien tengo dudas sobre este ejercicio. El enunciado dice claramente que la superficie es el «trozo sombreado de superficie cilindrica», con lo cual yo entiendo que es abierta porque en ningun momento dice que es frontera de ningún sólido. Ademas dice que hay que orientarla en la direccion del eje x positivo, con lo cual habría que proyectarla sobre el plano zy, y el recinto de integración sería un triangulo, asi que tampoco entiendo porqué usan cordenadas cilindrias. En fin, no entiendo bien lo que pide, pero con las condiciones que dije antes el flujo me da 8.
Saludos.
Pedro.
ese flujo que calculas pedro es a traves del plano , no del cilintro, estoy casi seguro que tomaron como normal (1,0,0) ahora si es abierta como es posible que la proyecccion quede un triangulo ??
Yo lo que veo en el dibujo es lo siguiente.. un cilindro cuya parte sombreada no se va al infinito , por eso digo que ese cilindro no es abierto , esta acotado por el plano z=4 y ademas en el primer octante…
Yo entiendo el sólido que ves vos. Pero no me parece que en ninguna parte del enunciado haga referencia a que la superficie sobre la que hay que calcular el flujo sea la frontera de ese sólido, sino la región sombreada del cilindro tal como muestra la imagen; y que el limite de z=4, el plano y+z=4 y el primer octante son como vos bien decis, para poder determinar ese trozo de cilindro.
Contestando tu primer pregunta, si proyectas ese trozo de cilindro (superficie abierta) en el plano yz, el recinto de integración es un triángulo (en el dibujo del enunciado se ve bastante claro) y la superficie sobre la que calculo el flujo no es un plano sino justamente el trozo de superficie cilíndrica.
Además, si la superficie en cuestión fuese la superficie cerrada frontera del sólido, tendría que estar sombreada en el dibujo la mitad de la tapa circular del cilindro (z=4), es decir la mitad que corresponde al primer octante.
Desde ya que todo esto es una opinión.
Saludos.
Pedro.
Sin animos de crear mas confusion, me parece que el E1, era un toque mas complicado resolverlo mediante la aplicacion del teorema de la divergencia, ya que la superficie era abierta y habia que calcular tres tapas para poder cerrarla, el cilindro esta cortado por la mitad por el eje y +. Otra de las tapas es la de abajo con el plano z+y=4 y la de arriba. El resultado según corrección del final es 8. Quedando como region de integracion la proyeccion sobre el plano zy un triangulo de base 4 y altura 4. A= (bxh)/2=16/2=8
El gráfico presta a confusiones gran problema para los que padecimos el final.
Saludos.
de la manera que estan sacando el flujo que les esta dando 8, no estan tomando en cuenta las inecuaciones que me definen el primer octante, o sea si no estuviese esa restriccion en el enunciado, estaria totalmente de acuerdo con uds y no aplicar el teorema de la divergencia directamente.. en ese caso tomaria directamente la definicion .
Estamos todos de acuerdo con que nos piden el flujo a traves de
o no ?
Absolutamente de acuerdo. Con esas inecuaciones la superficie en cuestión es una superficie abierta que pertenece al primer octante y cuya proyección sobre el eje yz es un triángulo.
una pregunta, como sacaste que h(1,2)=2f(1) es 6??
y de que sirve saber que (1,3) pertenece a f
fijate que el enunciado dice «el punto (1,3) pertence a la grafica de f» entonces f(1)=3 entonces cuando hago h(1,2)=2f(1) pero por los datos del enunciado sabemos que f(1)=3 entonces h(1,2)=2.3=6
me estoy respondiendo solo, me di cuenta 3 segundos despues de postear como era
Buenas, una pregunta,
en el E1, pregunta hacia donde esta orientado nunca entendí muy bien ese concepto, el resultado me dio 8 como a todos pero no se decir hacia donde?
en el E2, entiendo todo, f(1)=3 pero las f´(1) porque se cancelan? debe ser una pavada. Pero no me cierra. Después todo lo que vi esta bien.
Hola Leandro. Cuando vos obtenés el gradiente de la superficie estas obteniendo el vector normal de la misma punto a punto, y ese vector sería el que te marca la dirección del flujo. Entonces si tu gradiente es por ejemplo , en todos los puntos de la superficie que verifiquen x=2, y=2, el vector normal será (4,0,0), que tiene la misma dirección que el (1,0,0), es decir que la estás atravesando en el sentido de las x+.
, en todos los puntos de la superficie que verifiquen x=2, y=2, el vector normal será (4,0,0), que tiene la misma dirección que el (1,0,0), es decir que la estás atravesando en el sentido de las x+.
Si alguien puede aclararlo mejor sería de gran ayuda, yo tampoco lo tengo tan claro verdaderamente.
Pedro.
Hola buen, dia tengo una pregunta en el T2, en la integral como sabes de donde a donde va Z?
Saludos
obsrva que la divergencia nos da constante , entonces puede ir fuera de la integral triple
entonces puede ir fuera de la integral triple
pero te piden que lo hagas a traves del volumen de una esfera, entonces esa integral triple si la resolves te da la formula del volumen de la esfera
si queres resolverla planteando los limites de integración conviene que apliques coordenadas esfericas, llegas a lo mismo
entonces como era el e1?? a mi el flujo me dio 40
es 8 como insistio pedro… despues de ver las ecuaciones que limitaban la superficie , tenia toda la razon , yo cometi un error conceptual al aplicar divergencia 😦
no entendi como sacaste el intervalo de la r ahi,
la r<2
x^2 + y^2 = 4y
r^2=4*2*sen,
eso no me da r < 4sen
pero para que queres sacar el r Alex… no es necesario en este ejercicicio, si revisas las respuestas mas arriba de pedro y sebastian veras que se hace proyectando sobre el yz y te queda un triangulo
8 pi? u ocho solo da?
8 unicamente
entonces lo que habias puesto antes no va
«por error de transcripcion , en el E1 es
x^2+y^2=4y
por ende el limite en r es
0<r<4\sin\theta
y el flujo sera
16\pi
avisen si hay otro error mas porfi"
No va alex… no puedo editar aca , pero no va, es como dice pedro y sebastian .. igualmente da para confusiones ese dibujo , pero es asi como dicen mas arriba
perfecto, gracias por la explicacion
Podria subir el E1 desarrolado que no le entiendo. Gracias
seria mejor que lo desarrolles damian, perdon por ser molesto, me sumo al pedido de chr_go
buenas , disculpen , en el E3 , de donde sale la curva Y = -X^2 + 2 no entiendo ese punto inicial. gracias!
Hola Sebastían, sale que
sale que  o sea
o sea  , o sea
, o sea  . Por la condición de la recta tangente
. Por la condición de la recta tangente  sale que
sale que  y
y  , por lo tanto
, por lo tanto 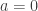 y
y 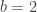 , de donde
, de donde 
De la ecuación diferencial
Saludos,
Damián.