Solución: (de la parte práctica)
1) a) Enuncie el teorema de derivación de la composición de funciones en forma matricial. Dada la superficie de ecuación
con
,
,
constante, utilizando el teorema determine el valor de
para el cual la recta normal a
en
resulta paralela al eje
.
La composición es del tipo
El vector normal a la superficie es entonces
Para que sea paralelo al eje los componentes
e
deben ser cero:
de ambos sale
y como
era el valor buscado.
b) Siendo con
, calcule la circulación en sentido positivo de
a lo largo de la curva plana de ecuación
Como puedo aplicar el teorema de Green.
uso el cambio de coordenadas a polares «trasladadas»
con
y su jacobiano es
la integral nos queda
2) a) Defina coordenadas polares. Aplíquelas para calcular la integral doble de en la región plana definida por
,
.
pasamos a coordenadas polares
con
su jacobiano es
transformo queda
o sea
transformo queda
b) Calcule el área de la región del plano que se muestra en la figura, limitada por el arco de curva de ecuación
con
y el segmendo de puntos extremos
y
Este ejercicio se podía hacer aplicando el teorema de Green para el cálculo de áreas planas, no olvidando de integrar el segmento de recta.
Pero también salía diréctamente con integrales dobles (en polares) de la siguiente manera:
El ángulo se ve que va de 0 a , y el radio es la distancia al origen, o sea que va desde cero hasta la norma de la parametrización
que es:
por lo tanto queda la integral doble en polares
En la siguiente imagen se ve sombreada la región cuya área calculamos

draw2d(
parametric(3*t*cos(t), 3*t*sin(t), t,0,2*%pi),
parametric(6*%pi - t, 0, t, 0, 6*%pi)
);
3) Siendo . calcule el flujo de
a través de la superficie abierta de ecuación
con
, indicando gráficamente la orientación que ha elegido para la superficie-
Este ejercicio se podía hacer con divergencia y sacando la tapa, o diréctamente como lo voy a hacer acá abajo. En este caso no voy a parametrizar la superficie sinó que voy a usar el método de integral de superficie implícita.
Primero averiguo como se intersecta la esfera con el paraboloide:
de la segunda despejo y reemplazo en la primera
de donde sale (no sirve) y
(sirve)
reemplazando en la segunda
o sea
es decir que la proyección sobre el plano es una circunferencia de radio 1.
defino
(la superficie es el conjunto de nivel 0 de G)
el vector normal a la superficie lo obtengo haciendo
Luego,
reemplazando con el valor de z sobre la superficie
nos queda
Por lo tanto el flujo pedido lo calculamos integrando en polares sobre la proyección en el plano de la superficie, que es la circunferencia unitaria, y nos queda
En el siguiente gráfico podemos ver en azul la parte de la esfera sobre la que calculamos el flujo (con normal hacia «arriba»), en celeste se ve parte de la continuación de la esfera, y en verde el paraboloide que sólo interviene para «recortar» la superficie.

draw3d(surface_hide = true,
xlabel = "x", ylabel = "y", zlabel = "z",
color = "light-blue",
parametric_surface(u*cos(v), u*sin(v), sqrt(5-u^2), u, 0, 1.5, v, 0, 2*%pi),
color = "blue",
parametric_surface(u*cos(v), u*sin(v), sqrt(5-u^2), u, 0, 1, v, 0, 2*%pi),
color = "green",
parametric_surface(u*cos(v), u*sin(v), 1+u^2, u, 0, 1.05, v, 0, 2*%pi)
);
4) Dado , calcule la circulación de
desde
hasta
a lo largo de la recta normal en el punto
a la superficie
definida implícitamente por
Este se podía hacer por función potencial ya que el campo es conservativo, de todas formas hay que averiguar los puntos y
. Yo lo voy a hacer de la forma directa, es decir sin usar función potencial.
defino
(la superficie es el conjunto de nivel 0 de G)
el gradiente es normal al conjunto de nivel, y por lo tanto a la superficie
la recta es entonces
con
luego y
derivo
la circulación pedida es




Hola Dami,
Con respecto al punto 1b que se aplica Green… al hacer las respectivas derivadas parciales, no quedan funciones g’x y g’y y por lo tanto no se pueden eliminar?
Muchas gracias.
Hola Rogelio, depende de una variable, digamos
depende de una variable, digamos 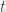 , es decir es una
, es decir es una  compuesta con una
compuesta con una  .
. es símplemente
es símplemente 



No, ese es un error muy común, fijate que
La derivada de
Lo que depende de dos variables es la compuesta
Por la regla de la cadena
Suerte,
Damián.
hola damian, yo soy agustin leira y hice el curso de verano con vos. me tire a dar el final y lo aprobe con 4 lo justo y lo necesario, aunq ahora que lo veo, viendo en que me equivoque debo decir que era bastante dificil. hice 3 bien perfectos, los primeros 3. los demas digamos que regular. queria agradecer por todo lo que nos explicaste en la cursada, se nota que sabes mucho del tema. saludos. agustin
Damian: respecto al ejercicio 2)b) ¿me podrias orientar como calcularlo por el teorema de green, mediante circulacion? Porque no le encuentro la vuelta al ejercicio. Se que es la suma de las 2 circulaciones, el area (la circulacion en el segmento y en la curva). Pero no se cual seria F(g(t)) y g'(t) en ambos casos.
Saludos,
Hola Guido, tal que
tal que  y
y  , por ejemplo
, por ejemplo 
![g_1 : [0, 2\pi] \to \mathbb{R}^2](https://s0.wp.com/latex.php?latex=g_1+%3A+%5B0%2C+2%5Cpi%5D+%5Cto+%5Cmathbb%7BR%7D%5E2&bg=ffffff&fg=333333&s=0&c=20201002) tal que
tal que  .
.
![g_2 : [0, 6\pi] \to \mathbb{R}^2](https://s0.wp.com/latex.php?latex=g_2+%3A+%5B0%2C+6%5Cpi%5D+%5Cto+%5Cmathbb%7BR%7D%5E2&bg=ffffff&fg=333333&s=0&c=20201002) tal que
tal que 
Ese ejercicio es un poco mas complicado de hacer por Green.
De todas formas, podés tomar cualquier
Como bien decis la curva la tenes que parametrizar por partes, para la parte «curva» ya te dan una parametrización
El segmento de recta lo podés parametrizar como
(es importante respetar la orientación antihoraria)
Suerte!
Muchas gracias!!
consulta, el normal del ejerc 4 no seria (3,1,2) ??
Lo revisé y me sigue dando si te referías a eso.
si te referías a eso.
si perdon da eso!
Hola dami una pregunta sobre el 1b yo lo hice de la siguiente manera
tomando obtengo la siguiente integral
obtengo la siguiente integral
¿ esta bien la función de la manera que la tome yo ?
de la manera que la tome yo ?
gracias
Ya me di cuenta del error, tome mal el t debería ir de
de todas maneras me gustaria tu opinion 😉
saludos
Lo veo bien 🙂
gracias dami 😉
Tengo una duda con el ejercicio 2b:
Teniendo:
x=3φcos(φ)
y=3φsen(φ)
¿El jacobiano no debería ser φ en vez de ρ? En cuyo caso el área daría 8π^3 en vez de 12π^3
Hola Gaby, ?. Igual fijate que ahí modifiqué la explicación de ese ejercicio. Yo usé polares así que el jacobiano me quedó
?. Igual fijate que ahí modifiqué la explicación de ese ejercicio. Yo usé polares así que el jacobiano me quedó 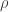 .
.
No entiendo del todo tu pregunta, porqué el jacobiano te queda
Saludos,
Damián.
en el 2a, porque uno de los limites de integracion de p es 0? no logro entender de donde sale
no entiendo porque en el 3, integras ro entre 0 y 1
ya entendi mi error, gracias
Hola Damian,
Mi nombre es Juan Cruz y quería consultarte una duda del punto 4.
El razonamiento lo hice igual que vos, solo que el gradiente de la superfice lo saque de manera implicita, y de ahi a que me da distinto. Podrías por favor aclararme esta duda?
Muchas gracias.
Saludos.
JC
Hola Damian, en el ejercicio 3.
La integral final me queda a integrar Raiz de 5 x Z (reemplazo Z despues por Raiz de 5-X^2-y^2)
Segui el metodo explicado en el FLAX, y no me queda todo dividido 2Z antes, no deberiamos hacer el gradiente de la superficie dividido la norma del gradiente y luego multiplicarlo por f?
Quedando asi f.n = raiz de 5 x Z
Sino no entiendo el metodo utilizado, gracias y saludos