
Respuestas:
T1) 12 orientado hacia
E1) Reemplazando en la fórmula de la función te quedan tres puntos críticos
El primero por el hessiano da minimo relativo . Los otros dos dan puntos silla.
E2) Sale fácil por rotor:
E3)
E4)

Respuestas:
T1) 12 orientado hacia
E1) Reemplazando en la fórmula de la función te quedan tres puntos críticos
El primero por el hessiano da minimo relativo . Los otros dos dan puntos silla.
E2) Sale fácil por rotor:
E3)
E4)
| Juani Rigada en 2º Parcial Curso de Verano… | |
| Santiago Orlando en Final 19/12/2017 | |
| damidami en Final 12/12/2017 | |
| Rochas (@agustinroch… en Final 12/12/2017 | |
| Emy Goicoechea en Final 12/12/2017 | |
| damidami en Final 20/07/2010 | |
| Rochas (@agustinroch… en Final 20/07/2010 | |
| Rochas (@agustinroch… en Final 19/07/2011 | |
| damidami en Final 19/07/2011 | |
| Rochas (@agustinroch… en Final 19/07/2011 | |
| damidami en Final 21/12/2009 | |
| Guido Paolini en Final 21/12/2009 | |
| damidami en Tp 3 Ej 3.c | |
| Guido Paolini en Tp 3 Ej 3.c | |
| Matias Isturiz en Final 24/05/2017 |
En los comentarios podés escribir expresiones matemáticas usando código ![]() .
.
Por ejemplo si escribís...
$latex 2 \int_0^4 dx \int_0^8 dz = 64 $
...se visualiza como:
Más información (en inglés)

Buenas en él E3) cuando te queda por resolver r √(3-2r^2) en la integral. No encuentro esa forma en la tabla de integrales. Solo vi r√(3-r^2) como haría en él final ? Por que no entiendo como ponen una integral que no esta en la tabla. Muchas gracias
Sale por sustitucion, llamas u=3-2r^2 hallas du y lo reemplazas
Buenas, no entiendo como llega a 12 en el punto T1.
Hola Agustin,
Fijate que la divergencia de f es cero. Luego el flujo total saliente sobre la frontera del solido formado por las dos superficies que te dan es cero, luego el flujo orientado ambas hacia arriba es el mismo (pues son igual en modulo pero de signo cambiado orientando saliente), es decir 12 pues es dato del enunciado para la segunda superficie.
Saludos,
Damian.
Gracias damian!
Hola a todos, consulta, en el E3) como sabe que ro va de 0 a 1.
si la proyeccion sobre el plano xy me da una circunferencia de radio raiz de 3/2?
muchas gracias,
saludos.
Hola Santiago, con el semicono
con el semicono  , de la segunda ecuación en la primera te queda
, de la segunda ecuación en la primera te queda  , o sea
, o sea 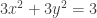 , o sea
, o sea 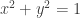 , de ahí que
, de ahí que 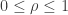 .
.
Al intersectar el elipsoide
Saludos,
Damián.
Hola, en el ejercicio E4, la solucion no seria: -1-e^(-4x)+2x
Gracias, saludos
Hola Lucio, cosa que deberia para tener recta tangente
cosa que deberia para tener recta tangente  en
en  .
.
No, porque lo que propones como solución no cumple que
Saludos,
Damián.
Buenas!
En T1, queda
flujo Scerrada = 12 + flujo S1 (donde S1 es la tapa que queremos averiguar)
Como divf = 0, el campo es solenoidal y el flujo Scerrada = 0, lo que da que flujo S1 = -12
mi consulta es, ¿Queda 12 ya que esta orientado saliente (z-) y te lo piden orientado en z+?
o sea, ¿Cambia de signo al cambiar el sentido de orientación?
Hola Demian, si, es como decis.
Hola, consulta del E3), cómo sé que tita se evalúa entre pi/4 y 5.pi/4? Entiendo lo de pi/4 ya que es x=y, pero cómo determino el otro valor?
Hola Mercedes,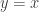 , son 180º mas, es decir
, son 180º mas, es decir 
Es por la misma recta
Saludos,
Damián.