No tengo las respuestas, y ando con poco tiempo, así que pongo sólo el enunciado.
Siempre pueden compartir sus respuestas en el blog para ver si a todos les dan los mismos resultados.
-
Únete a otros 268 suscriptores
Comentarios recientes
Juani Rigada en 2º Parcial Curso de Verano… Santiago Orlando en Final 19/12/2017 damidami en Final 12/12/2017 
Rochas (@agustinroch… en Final 12/12/2017 Emy Goicoechea en Final 12/12/2017 damidami en Final 20/07/2010 
Rochas (@agustinroch… en Final 20/07/2010 
Rochas (@agustinroch… en Final 19/07/2011 damidami en Final 19/07/2011 
Rochas (@agustinroch… en Final 19/07/2011 damidami en Final 21/12/2009 Guido Paolini en Final 21/12/2009 damidami en Tp 3 Ej 3.c Guido Paolini en Tp 3 Ej 3.c Matias Isturiz en Final 24/05/2017 LaTeX
En los comentarios podés escribir expresiones matemáticas usando código
 .
.Por ejemplo si escribís...
$latex 2 \int_0^4 dx \int_0^8 dz = 64 $
...se visualiza como:
Podés practicar en este post.Más información (en inglés)




Gente, estoy estudiando para rendir el lunes 21.02.2011 y resolví algunos ejercicios de este final. Les paso los resultados y cuando tenga mas tiempo el desarrollo de cada uno. No lo tomen como palabra santa, pero si todos llegamos al mismo resultado, por algo será, no ??
Acá van:
2a) Las derivadas parciales de f se anulan simultáneamente en (x,y)=(0,0) y como Im(f)=Reales positivos incluido el cero, en (0,0) existe mínimo local y absoluto.
3) Volumen = pi (usando coordenadas cilíndricas sobre el eje y, es decir, x=ró coseno; y=y; z=ró seno)
4) flujo = -512/35 (usando flujo por definición, proyectando sobre el plano xz y sin realizar cambio de variables)
Hola!! Escribo lo q me dió algunos ejercicios así lo comparamos
1)b) rta: y^2=2x^2 + 2 ( el campo f me quedó f(x,y)=(y^2,2xy) )
2) a) No puedo usar hessiano, verdad? porque el pto critico es(0,0) pero al reemplazar en el hessiano, no está en el dominio….si no uso hessiano,como lo resolvieron?
2)b) rta: hay pto de ensilladura,por lo tanto no hay extremo (H=-288 <0)
3) rta: 7/4 pi (use coordenadas cilindricas)
Hola Andrea,
El 1b me quedó igual que vos.
El 2a me pasó eso, que no puedo usar el Hessiano porque en (0,0) no está definido el campo. El análisis que hicimos con un amigo es referido a la definición de extremos. Tenemos las siguientes condiciones:
– para todo (x,y) perteneciente a los Reales, el conjunto Imagen son los Reales positivos con el cero
– en (0,0) las derivadas parciales se anulan simultáneamente
Y por definición:
para todo (x,y) perteneciente a los Reales existe el punto (0,0) tal que f(0,0) (0,0) mínimo absoluto.
Por el resto de los puntos, el viernes subo mis resoluciones así comparamos o me corregís porque la respuesta del 3) 7/4 pi es mas estética que la mia, jaja.
Saludos y ojalá alguien mas pueda aportar.
Andrea, te pido si me podes explicar como llegas a ese resultado en el 1 b, ya que no se si capaz estoy haciendo algo mal yo.
Hasta donde tengo entendido las lineas de campo y las potenciales son ortogonales, por lo que lo que hize fue calcular la derivada del campo potencial: c = xy^2 , despues a y’ la reemplazo por 1/y’ . despues integro, y esa deberia ser la ecuacion de las lineas de campo.
Ahi deberia calcular el valor de C y listo… pero no me da ni cerca tu valor…
Es asi??
gracias, Leo
Hola fede,
Gracias por la explicacion del 2)a
El 2)b ¿nos coincide?
El 3) usé como vos, coord cilindricas sobre el eje y. Comparemos los integrales, a mi me quedo: fi entre 0 y pi/2 ,ro entre 0 y raiz(2) y y entre 0 y 4-ro^2 cos^2fi
El 4) me dio 256/35 . Hice la Integral doble de x^4 dxdz
Saludos
yo rendi y me saque un 8, creo q me confundi solo en el 2b porque puse mal un signo 😛 …
el 3 y el 4 me dieron igual q a fede.
andrea fijate en el 3 que Y no va desde 0. va desdela ecuacion de abajo q seria cos^2 + 2 sen^2 ….
Gracias!
lo corregi y ahora si me da pi el pto 3.
El pto 4 me di cuenta q cometi un error, y ahora me da 512/35 (me quedo positivo) Los limites de integracion me quedaron x entre -2 y 2, z entre 0 y 4-x^2…¿porqué te queda negativo?
En resumen, me están quedando estos resultados:
1)b) rta: y^2=2x^2 + 2
2)a) rta: (0,0) existe mínimo local y absoluto
2)b) rta: hay pto de ensilladura,por lo tanto no hay extremo
3) rta: pi
4) rta: 512/35
le dio negativo porque uso el normal al reves (2x,-y,0) ,, es lo mismo si lo indicas en el grafico
yo use la normal (-2x, 1, 0)….¿estaría bien los 2 resultados?
no me acuerdo qué normal usé, no tengo los desarrollos conmigo, pero si hayás el resultado con una normal «n» y después hacés lo mismo con una normal «-n» debería darte el mismo flujo pero con distinto signo.
Integral doble [ f. (-n) ].ds = – Integral doble [ f. n ].ds
Acá van mis desarrollos de los puntos 3 y 4:
Punto 3)
La figura es, desde el origen parte un paraboloide elíptico y=x^2 + 2z^2 hasta cruzarse con la parábola y=4-x^2.
La proyección que usé fue sobre el plano xz y lo que se ve es la intersección de las 2 superficies, quedando un cuarto de circunferencia de radio raiz cuad de 2.
Ergo, usé coord cilíndricas parametrizadas de la sig. manera:
_
| x= ro . cos (tita)
<| y=y
|_ z= ro . sen (tita)
Límites:
0 < o igual a tita < o igual a pi/2
0 < o igual a ro < o igual a raiz cuad de 2
(ro)^2.cos^2(tita) + 2.sen^2(tita)
< o igual a y Integral entre [(ro)^2.cos^2(tita) + 2.sen^2(tita)] y [4-(ro)^2.cos^2(tita)] dy = 4-2.(ro^2)
=> Volumen = Integral entre 0 y [pi/2] d(tita) x Integral entre 0 y raiz cuad de 2 de [4(ro) -2(ro^3)] d(ro)
=> Volumen = [pi/2] x [2]
=> Volumen = pi
Punto 4)
Flujo por definición:
Integral doble sobre superficie E de campo vectorial f x versor normal a E x diferencial superfice
|| f.n ds
´´E
E = x^2 – y
f(x,y,z) = (xy, 3yx^2, xz)
n = Gradiente de (E) / || Gradiente de (E) ||
Gradiente de (E) = (2x, -1, 0)
|| Gradiente de (E) || = raiz cuad de (4x^2 + 1)
ds = dx.dz / |cos n.y|
|cos n.y| = 1 / raiz cuad de (4x^2 + 1)
=> [f.n] / |cos n.y| = 2yx^2 – 3yx^2 = -y.x^2
=> Flujo = Integral entre -2 y 2 de (-y.x^2) dx x Integral entre 0 y [4-x^2] dz
=> Flujo = Integral entre -2 y 2 de (-x^2.x^2) dx x Integral entre 0 y [4-x^2] dz
=> Flujo = – Integral entre -2 y 2 de (x^4).(4-x^2) dx
=> Flujo = – Integral entre -2 y 2 de (x^4).(4-x^2) dx
=> Flujo = – Integral entre -2 y 2 de (4x^4 -x^6) dx
=> Flujo = – [ (4.2^5)/5 – (2^7)/7 – ( (4.(-2)^5)/5 – ((-2)^7)/7 ) ]
=> Flujo = – [ (4.2^5)/5 – (4.2^5)/7 + (4.2^5)/5 – (4.2^5)/7 ]
=> Flujo = – [ (4/5).2^5 – (4/7).2^5 + (4/5).2^5 – (4/7).2^5 ]
=> Flujo = – [ (8/5).2^5 – (8/7).2^5 ]
=> Flujo = – [ (16/35).2^5 ] = – (32 x 16) / 35
=> Flujo = – 512/35
Hola Fede,
No leí tus resoluciones pero intervengo nomás para recordar que pueden usar código LaTeX para escribir ecuaciones en los comentarios.
Por ejemplo si escribo
$latex f(x) = \frac{x^2}{2}$
se muestra la imagen

Cuando te acostumbras no es difícil escribir los comandos necesarios, en internet hay bastante documentación, y sería más fácil de leer la resolución para los demás.
Comento esto por si no lo sabías nomas,
Suerte,
Damián.
Gracias Damián, no recordaba que podía usar LaTex.
Tu comentario suma y eso es lo importante.
Saludos!
Que tal, si bien puedo equivocarme, respecto al punto 4, utilizando el versor derivado de , tal como lo hizo Fede, al aplicar el modulo al coseno director j, el resultado da siempre negativo (es decir, la componente «y» siemre es negativa si usamos ese versor), por lo que termina quedando 512/35. Corrijanme si me equivoco, saludos.
, tal como lo hizo Fede, al aplicar el modulo al coseno director j, el resultado da siempre negativo (es decir, la componente «y» siemre es negativa si usamos ese versor), por lo que termina quedando 512/35. Corrijanme si me equivoco, saludos.
Leo, no entiendo cómo haces para que [f.n] / |cos n.y| te de positivo. O a lo mejor te entendí mal.
El valor negativo me queda desde esa fórumla. Usé el versor con componente «y» negativo y el módulo del coseno director es siempre positivo (por ser módulo), de ahí me queda que, del producto escalar, la suma de los numeradores de la fracción (previo a dividir por el módulo del coseno director) me queda:
(2-3).y.x^2
y esto me queda
(-1).y.x^2
Ese «-1» es el que traslado hasta el final del ejercicio y el resto de las cuentas nunca me genera un valor negativo como para anular ese «-1».
Espero haber aclarado mi forma de resolver. Si entendí mal lo que quisiste decir, por favor aclarámelo que para esta materia hay que tener muy claros los conceptos.
Saludos y gracias por el aporte !
Entendiste bien Fede, me confundí sobre el concepto de módulo. El resultado es negativo (usando el versor con componente «y» negativa). Nada más que decir, suerte el lunes!.
Mis resultados:
1)b) y^2=2x^2 -1 (Andrea, a mi me queda la constante igual a 1 luego de reemplazar por el punto (1,2)). Antes del reemplazo tengo x^2 + c =y^2/2
Alguien mas pudo hacer este punto?
3) pi
4) con normal = (-2x, 1, 0) tengo que integrar x^4 como comento Andrea, tengo que terminar las cuentas.
Copie mal el resultado de 1)b) lo correcto seria: x^2=y^2 -1
Saludos
Nico, te pido si me podes explicar como llegas a ese resultado en el 1 b, ya que no se si capaz estoy haciendo algo mal yo.
Hasta donde tengo entendido las lineas de campo y las potenciales son ortogonales, por lo que lo que hize fue calcular la derivada del campo potencial: c = xy^2 , despues a y’ la reemplazo por 1/y’ . despues integro, y esa deberia ser la ecuacion de las lineas de campo.
Ahi deberia calcular el valor de C y listo… pero no me da ni cerca tu valor…
Es asi??
gracias, Leo
Yeti, no se si tipeastes mal pero para encontrar la familia ortogonal tenés que reemplazar por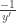 en vez de
en vez de 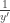
Suerte,
Damián.
si, es asi, me equivoquè tipeando.
Es asi la forma de resolucion? porque sino debe ser un error mio en el despeje, pero si es esa la forma en que se resuelve, me quedo mas tranquilo.
Gracias! Leo
Yo rendi el lunes pasado este final, en el punto 2)a) No hay extremo por que las derivadas parciales son distintas. Eso me dijo la profe. Y, es real lo que dice alguna de las chicas aca creo q Andrea. Al reemplazar cuando hago el hessiano me doy cuenta que las derivadas no existen fijense!!!
Hola Lucila!
Coincido con vos en lo del pto 2a, ya que si lo graficás te quedan 2 conos (1 sobre las Y>=0 o otro sobre las Y<=0).
Y como se extiende hasta el infinito creciendo sobre el eje Y, no tenés ningun extremo.
Por otro lado, el pto (0,0) que es el del conflicto no pertenece al dominio de f'x ni de f'y asi que no podrías evaluar al gradiente en el origen.
Conclusion, no tiene extremos.
Claro!!! No es que las derivadas parciales son distintas es que tienen que dar cero ambas sino fijense donde dice extremos en la pagina 32 de la gui de tp donde estan las condiciones necesaria y suficiente para la existencia de extremos. Es muy importante!
Hola Lucila y Gustavo, (la parte con
(la parte con 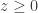 ).
).
Intervengo porque me parece que se están confundiendo en el ejercicio 2a)
La función si la grafican es un especie de semicono sobre el eje
La función es diferenciable en todo , es decir en cualquier punto menos en el origen, y en ninguno de esos puntos el gradiente se anula.
, es decir en cualquier punto menos en el origen, y en ninguno de esos puntos el gradiente se anula.
Pero no hay que olvidarse de fijarse si en los puntos donde la función no es diferenciable se produce o no extremo.
En el origen se tiene y para cualquier otro punto
y para cualquier otro punto  se tiene
se tiene  , por lo tanto la función presenta un mínimo absoluto (y relativo) en sentido estricto en el origen. (Había que usar la definción de extremo).
, por lo tanto la función presenta un mínimo absoluto (y relativo) en sentido estricto en el origen. (Había que usar la definción de extremo).
Las condiciones necesaria (gradiente nulo) y suficiente (con el hessiano) se aplican sólo en los puntos donde la función es clase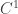 y
y  respectivamente.
respectivamente.
Suerte!
Damián.
Una duda, Como resolvieron el 2b)? Se realiza el Hessiano derivando el polinomio de Taylor? Porque lo hice de esta forma y no me da -288. Desde ya muchas gracias
A mi tampoco me da -288 sino 144.
1) obtendo P»xx(x,y), P»xy(x,y) y P»yy(x,y).
2) Luego obtengo el Hessiano evaluado en (-1,2), o sea, los polinomios derivados anteriormente evaluados en el punto ya que P» = F» en el punto.
me da 144, me fijo en P»xx(-1,2), que me da 24, por lo tanto tengo un MINIMO.
Martin a mi me da lo mismo que a vos, tiene un minimo relativo