Comentarios recientes
Juani Rigada en 2º Parcial Curso de Verano… Santiago Orlando en Final 19/12/2017 damidami en Final 12/12/2017 
Rochas (@agustinroch… en Final 12/12/2017 Emy Goicoechea en Final 12/12/2017 damidami en Final 20/07/2010 Rochas (@agustinroch… en Final 20/07/2010 Rochas (@agustinroch… en Final 19/07/2011 damidami en Final 19/07/2011 Rochas (@agustinroch… en Final 19/07/2011 damidami en Final 21/12/2009 Guido Paolini en Final 21/12/2009 damidami en Tp 3 Ej 3.c Guido Paolini en Tp 3 Ej 3.c Matias Isturiz en Final 24/05/2017 LaTeX
En los comentarios podés escribir expresiones matemáticas usando código
.Por ejemplo si escribís...
$latex 2 \int_0^4 dx \int_0^8 dz = 64 $
...se visualiza como:
Podés practicar en este post.Más información (en inglés)
Análisis Matemático II 
Hola!
El pto 1 a) me dio x-4y+3z+5=0
El pto 2 a) me dio pi
Coincido con alguien? En un rato hago los demás puntos y los escribo para comparar!
Saludos!!
Andrea
Si! el 1 a) me dio lo mismo que vos, x-4y+3z+5=0
el 2 a) no lo se encarar… tirenme una punta!!
Andrea:
Tengo problemas para terminar el 1 a) primero necesito sacar el prod vectoria de X’u y X’v
$latex X’u (vectorial) X’v
Luego despejo u y v con el punto (1,3,2)
u-v² = 1
u+v = 3
uv = 2
me quedan u=2 y v=1 para reemplazar en el vector resultante del producto vectorial anterior. Me queda como resultado (1, -4, 3), que por lo que veo, es lo que te quedó a vos.
El problema es que no puedo hallar la forma de encontrar ese 5 que te quedó en el resultado final.
Eso es reemplazando algo en algun lado?
Gracias!
Gustavo:
te faltaria hacer
(X-A).N=0
((x,y,z)-(1,3,2)).(1,-4,3)=0
cuentas y da x-4y+3z+5=0
El punto 4 me da la curva integral una recta incluida en el plano y-x+2, el area de ellos no sería 0 porque la curva no delimita ninguna region?
las curvas del pto 4 me dan así:
y = x – 2 ; y = -x² + 4
y el área = 125/6 ( integrando así: -3 < x < 2 ; x-2 < y < -x²+4 )
alguno puede corroborar?
gracias!
El punto 4 nos da lo mismo Gerardo
Lo mismo! 125/6
El pto 4 me da como ustedes, 125/6 !!
El punto 3:
El punto 3 me dio 18,75 el área, aunque tuve que hacer un cambio de variable. Si lo saco directo por algun ploteador de integrales da casi igual, pero no estoy seguro que los límites de integracion que haya elegido sean exactos.
a mi me da lo mismo
Perdon, el comentario anterior mio esta mal e incompleto. Mis disculpas
El punto 3:
igualando
obtengo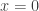 
por lo tanto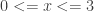 
en cuanto a la superficien me queda que:
así que la integral va a ser igual a
que sería
Si lo mando directo al wolframalpha para que me calcule la integral me da algo de 18,37, hice un cambio de variable siendo
y me dio 18,75.
A alguien le coincidio el resultado?
El pto 3 me quedó igual que vos, hice sustitucion de la misma manera y me da como resultado 18,67
Revise las cuentas de la integral y me da aproximadamente 18,67
Alejandro:
El 2)a hice esto: interseccion entre las 2 sup me queda que la curva C es x^2 + y^2 = k^2
Luego usando el teorema del rotor rotf.n=(2x,3y,5/z) .(0,0,1)=5/z
Entonces te queda la integral doble de 5/z dxdy
z =k^2, luego se pasa a polares y calculando la doble integral me quedo pi como resultado.
El 1 b) alguien entiende como hacerlo?
Gracias!
te consulto, porque capaz que entendi mal tu resolución:
z no debe ser igual al la z de la superficie, debido a que la que elegiste es plana? si proyectas al plano x,y no deberías erradicar la z de las integrales?
Yo lo hice de la siguiente manera:
igualo las superficies y me queda la curva tal como la tuya.
de paso saco los limites de integracion, puesto que
y esto es
luego elijo la superficie z=5, así al reemplazar z en la curva se cancela.
y me termina quedando por barrow
A mi no me da
como a vos… pero no estoy seguro que la logica de mi resultado sea correcto, por eso te pregunto.
perdon, donde dice formula does not parse se debe a que todavia no uso bien el LaTex
deberia decir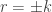
y barrow queda![2\pi \left [\frac{r^2}{2}\right]_{-k}^{k}](https://s0.wp.com/latex.php?latex=2%5Cpi+%5Cleft+%5B%5Cfrac%7Br%5E2%7D%7B2%7D%5Cright%5D_%7B-k%7D%5E%7Bk%7D+&bg=ffffff&fg=333333&s=0&c=20201002)
Hola Marin,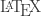
. 😉
Edité tu comentario para corregir el código latex como decías.
Me parece que en wordpress no se le puede agregar colores a partes distintas de un mismo comando, sólo al comando entero. Igual venís bastante bien con los comandos
(Aclaro que no estoy leyendo la resolución)
Suerte,
Damián.
Martin, el enunciado dice k positiva, aparte no tendria sentido considerar un -k si k es el radio del circulo de la region de integracion.
Lo hice ahora como Andrea y se simplifican las K^2 , creo que con eso verificas que no depende de K. Pero al final me dio 5 pi
Andrea, fijate que una vez que te queda la integral doble de 5/z, tenes que reemplazar Z por K² porque tenes que sacarte esa variable de encima.
Al reemplazarla de esta manera te quedaria integral de 5/K² lo que ayuda a eliminar al ro² / 2 que te queda una vez que integras.
Finalmente te quedaria 5 multiplicado por integral entre 0 y 2pi (lo escribo por si no me sale el latex 😛 )
\latex 5 \int_{\theta =0}^{2\pi }\int_{r=0}^{k} \frac{1}{k^2}r dr d\theta = 5\pi
A ver ahora si me sale el latex
Gustavo,
Te faltó cerrar el comando latex con $
Ya te lo corregí en tu comentario de acá arriba.
Suerte,
Damián.
Gustavo gracias! Me comi el 5,,,sisi , el pto 1a) me da 5pi
En polares no puede haber radio negativo, asi q no puede ser q el limite de integracion quede desde -k a k , queda desde 0 a k
por otro lado, eso de reemplazar z por 5 no entiendo porque lo haces, para mi z = k^2, luego cuando resolves se va a simplificar ese k^2
(cuando puedas me tiran una idea del 1 b y del 2 b q me estan costando!!!)
Si, me di cuenta mientras hacía el 2b, al venir a la compu para corregirme ya me habían ganado de mano uds 😛
Menos mal que estan del otro lado.
Lo de reemplazar la variable que no aparece en los diferenciales a partir de la superfecie unicamente fue algo que siempre hice en la cursada. En este caso no hacía falta igual.
Hola quisiera saber si alguien pudo hacer el ejercicio 2.b) que no se como terminarlo. Lle gue a dejar expesado: fi(x) – fi'(x)=0. pero no se como resolver esa ecuacion diferencial, va en realidad me dio cero, pero no esta bien. Si alguien sabe como se hace se lo agradezco.
El pto 2 b)
![[\varphi(x)= 2e^x]](https://s0.wp.com/latex.php?latex=%5B%5Cvarphi%28x%29%3D+2e%5Ex%5D&bg=ffffff&fg=333333&s=0&c=20201002)
me da como respuesta
Calculando la ED
![[\varphi'_{y}(x)y=\varphi(x)]](https://s0.wp.com/latex.php?latex=%5B%5Cvarphi%27_%7By%7D%28x%29y%3D%5Cvarphi%28x%29%5D&bg=ffffff&fg=333333&s=0&c=20201002)
Andrea,
Tenés que agregar un espacio después de escribir $latex para que parsee bien el comando. Y no hacen falta los corchetes (no se para que los agregastes).
Ya te lo corregí yo el comando latex.
Suerte,
Damián.
Damian gracias, los corchetes los puse de mas!
Saludos
Bueno no salio en latex…..
la respuesta del 2 b) me dio fi= 2e^x
resolviendo la ed fi(x) – yfi’(x)=0 siendo la y=1 en la superficie
Hola Andrea, gracias por constestar, ya lo resolvi y me dio como a vos !! Saludos.
hice el 1b) pero no se si está bien
Primero desparametrizo la superficie que queda
despues hago la intersección entre las 2 superficies para obtener la curva
y
paremetrizo la curva
![g(t)=(4-t^2),\sqrt[]{(4-t^2)^2+t^2},t)](https://s0.wp.com/latex.php?latex=g%28t%29%3D%284-t%5E2%29%2C%5Csqrt%5B%5D%7B%284-t%5E2%29%5E2%2Bt%5E2%7D%2Ct%29&bg=ffffff&fg=333333&s=0&c=20201002)
obtengo vector tangente
![g'(t)=(4-2t),\frac{8-2t^2-2t+2t}{\sqrt[]{(4-t^2)^2+t^2}},1)](https://s0.wp.com/latex.php?latex=g%27%28t%29%3D%284-2t%29%2C%5Cfrac%7B8-2t%5E2-2t%2B2t%7D%7B%5Csqrt%5B%5D%7B%284-t%5E2%29%5E2%2Bt%5E2%7D%7D%2C1%29&bg=ffffff&fg=333333&s=0&c=20201002)
Si
satisface la ecuacion del plano y = x – z por lo tanto lo intersecta
como llegas a que la superficie desparametrizada es y^2=x^2+z^2 ?
no seria x^2+ z^2=5^2 (circunf con radio 5) ?
x = u cos(v)
y= u
z = u sen(v)
Si y = u y u va entre 0 y 5 osea es un cono eliptico que esta definido entre 0 y 5, lo que vos decis es un cilindro
Pregunta, cuando derivas g'(t), la primer componente no debería quedar 2t? en vez de 4 – 2t, ya que 4 es una constante y se anularía al derivarse
Si, me equivoqué, está mal derivado. Pero creo que el procedimiento es así…
Acerca del punto 3, también me dio ~18,65, directamente en cartesianas y sin aplicar ningún cambio de variables.
Coincido con Gustavo sobre el punto 2a, la misma resolución, solo que al ser un circulo, no es necesario usar coordenadas polares, es simplemente la superficie de un circulo (o esto es obligatorio?). Aclaro por las dudas, el resultado me dio 5π.
Hola alguien me podría decir que estoy haciendo mal en mi resolución del 2b, que no termino de entender como llegar al resultado que les da a uds?
La ecuacion diferencial que necesitamos sacar es: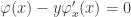
integrando me queda
aplicando el numero e
llamo a $latex $e^{C} = K $
y me queda
claramente no es nada parecido :S
mira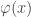
es funcion de x asique la derivada es respecto a x no respecto a y. 
En realidad y lo reemplazas por 1 que es lo que vale en la superficie.
Igualmente a mi tambien me da distinto que a ellos, porque yo hago
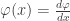
entonces
como f(0,1,1) = (2,0,2) entonces
C = ln 2
me queda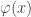
= e^( x + ln 2 )
a mi me queda igual que a Martin. Con C=2 … o sea
Mmmm… Alejandro, me pierdo un poco en tu resolución por lo siguiente:
Cuando tenemos una ecuación diferencia de tipo, por ejemplo, y’ + y = x
ahora bien, imaginemos que en este caso
eso nos daria que
entonces por qué a vos te da que
??
Entiendo que
tiene una x metida entre paréntesis, pero no se si en ecuaciones diferenciales eso deberiamos tenerlo en cuenta, ya que 
la podriamos llamar z como lo hice mas arriba.
Gustavo, a mi C me dio 1, yo lo saqué así, por casualidad es un error de calculo o lo sacaste de otra manera?
tengo la solucion gral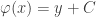
sabemos que f(0,1,1) = (2,0,2), por lo tanto evaluando f en los puntos nos queda que
por lo tanto ya de la primera componente evaluada, sacamos que
entonces, volviendo a la solucion general
por lo tanto la solucion particular nos quedaría
Hola Alejandro/Martin/Gustavo.
Les comento como resolvi el ejercicio en el examen.
Una vez encontrada la ED yfi'(x)-fi(x) = 0 , como bien dijo Alejandro reeplazamos la y por 1, pero luego resolvemos como si fuera una ED de 2do grado. Entonces lo primero es armar el polinomio característico:
r – 1 = 0 => r = 1
y la SG nos quedaria asi: y = C1 e^x
lugo con el dato f(0,1,1)=(2,0,2) usamos el primer valor: cuando la x vale 0 la imagen vale 2, entonces:
2 = C1 e^0 => C1 = 2.
Solución: y = 2e^x a esto lo llamamos fi.
me da lo mismo que a Fede y fijate que si tenes lo que puso Alejandro y no salio es lo mismo
Martín,
¿
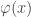no debería ser función de x?
saludos!
En el comentario de arriba mas o menos explico esa duda mia. Yo tampoco estoy seguro
Si vos tenes en ec. dif
el hecho de que hagas
responde a que estas viendo a y como funcion de x osea
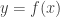
en este caso
mmm… realmente tengo un problema con las fracciones en latex y rindo en un toque asi que no puedo ver bien ahora como va, pero creo que por mas que salio mal se entendio. phi(x)=d phi/ dx
saludos
Alguien puede tirar alguna punta del 1 B ?
Estoy un tanto trabado con ese punto y la verdad que me debo estar trabando en alguna boludez…
Gracias!!
bueno, lo que hize, que no se si es lo correcto es calcular la normal a la primera superficie en el punto 0,2,2 y despues calculè la normal en la superficie y= x – z .
como no son paralelas, entonces doy por hecho que va a cortar seguro.
Hola Leo, como estas? cursamos juntos algunas materias que obviamente no recuerdo.
Te comento lo que hice en este:
_
Primero hay que «desparametrizar» X . Esto me quedo
y = raiz(x^2 + z^2)
La unica manera que encontre para chequear que este bien es parametrizar este resultado, y creo que esta bien por que a diferencia del resultado que proponen mas arriba al poner y^2 en el primer termino, estan tomando los y negativos, cosa que esta mal.
Una vez que tenemos las dos superficies debemos hallar la intersección, esto lo hacemos despejando z por ejemplo, las igualamos y parametrizamos. Me quedo asi:
g(t):( t , raiz( t^2 – t + 4 ) , raiz( 4 – t ) )
Si lo evaluamos en el punto en cuestión (0,2,2), o sea t=0, nos da el mismo punto (0,2,2), o sea que esta bien.
calculamos g'(t) que no escribo para que no quede ilegible ya que no uso el latex, pero si evaluas g'(t) te debería dar (1,-¼,-¼)
La ecuacion vectorial de la recta tangente nos queda:
_
X : (0,2,2) + λ(1,-¼,-¼)
Si λ vale 8/3, entonces satisface la ec del plano y = x – z
Hola! No encuentro de donde leer sobre «reduccion de orden en ED» lo encontraron en flax?
para el pto 4 hay q resolver
xy» – y’ = 0
si hago u=y’ u’= y» y luego hago
xu’ – u = 0 resuelvo esta ED….esto es «reduccion de orden»?
Gracias!
si, tengo entendido que a eso se le llama reducción de orden
saludos
para mi es asi el 1 b.
Hago interseccion entre las 2 superficioes
parametrizo la curva
![g(t)=(4-t^2,\sqrt[]{(4-t^2)^2+t^2},t)](https://s0.wp.com/latex.php?latex=g%28t%29%3D%284-t%5E2%2C%5Csqrt%5B%5D%7B%284-t%5E2%29%5E2%2Bt%5E2%7D%2Ct%29+&bg=ffffff&fg=333333&s=0&c=20201002)
obtengo vector tangente
![g'(t)=(-2t,\frac{2(4-t^2)-2t+2t}{\sqrt[]{(4-t^2)^2+t^2}},1)](https://s0.wp.com/latex.php?latex=g%27%28t%29%3D%28-2t%2C%5Cfrac%7B2%284-t%5E2%29-2t%2B2t%7D%7B%5Csqrt%5B%5D%7B%284-t%5E2%29%5E2%2Bt%5E2%7D%7D%2C1%29+&bg=ffffff&fg=333333&s=0&c=20201002)
![g'(t)=(-2t,\frac{8-2t^2}{\sqrt[]{(4-t^2)^2+t^2}},1)](https://s0.wp.com/latex.php?latex=g%27%28t%29%3D%28-2t%2C%5Cfrac%7B8-2t%5E2%7D%7B%5Csqrt%5B%5D%7B%284-t%5E2%29%5E2%2Bt%5E2%7D%7D%2C1%29+&bg=ffffff&fg=333333&s=0&c=20201002)
obtengo la recta
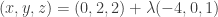
Alejandro:
A mi me queda -8/3
Fijate que en la g'(t) el 2do termino te falta algo , cuando derivas (4-t^2)^2 te deberia quedar 2(4-t^2).(-2t)
Yo encontré una solución un poco más fácil pero más vaga al mismo tiempo. Solo puedo demostrar que SI corta al plano, pero no donde.
Lo hice así…
con el producto vectorial de las derivadas parciales evaluadas en el punto obtengo la normal al cono en el punto (0, -2, 2).
Después despejo la ec. cartesiana del plano y obtengo la normal del plano que debería estar cortando (1, -1, -1).
Luego verifico que N1 != k*N2
de todas fromas me gustó mucho más tu resolución, pero creo que la mía es safable… que opinan?
Gerardo! yo me presente al examen lo único que se me ocurrio en ese momento fue eso (comparar gradientes) y cuando vi lo que me corrigieron habia una GRAN cruz en ese ejercicio y se leia: «NO RESUELVE»
Asi que por mas valida que nos parezca no es la solucion que los hace feliz. Por mas que el enunciado en ningun lugar dice que hay que hallar la recta ni nada parecido.
Saludos!
yo puse todo funcion de Xpongo lo que queda por si alguno lo hizo asi puesto que en el punto X=0 y te queda
la recta seria
aca te das cuenta de que y=z siempre, busco x e y
cuentas…
punto comun a recta y plano
Saludos
PD: ese 8/3 que me dio a mi nada que ver con el que viene de la otra parametrizacion calculo
bueno para la primera vez que uso latex me quedo con algun eror obvio.
me queda 2y=x porque z=y en mi parametrizacion y lo que dice frac8/3 era
8/3 y 4/3
mmm… a ver ahora
$A = (\frac{8}{3} , frac{4}{3} , frac{4}{3})$
Gente, hoy dandole un segunda vuelta de rosca al ejercicio me di cuenta que se puede resolver igual que ej 12 te TP 6 seguro ya lo tienen resuelto o por ahi Dami lo tiene en esta pagina. lo que se hace es plantear
&latex F(X)= x^2+y^2-z^2 = 0 $
&latex G(X)= x+z^2-4 = 0 $
sacas los dos gradientes de esto, hace producto vectorial y te queda la normal al plano
&latex Rt(X)= \lambda (16,-4,-4) + (0,2,2) $
&latex x= 16\lambda$
&latex y= -4\lambda +2 = z$
&latex \lambda= \frac 1 6$
Gente, hoy dandole un segunda vuelta de rosca al ejercicio me di cuenta que se puede resolver igual que ej 12 te TP 6 seguro ya lo tienen resuelto o por ahi Dami lo tiene en esta pagina. lo que se hace es plantear
&latex F(X)= x^2+y^2-z^2 = 0 $
&latex G(X)= x+z^2-4 = 0 $
sacas los dos gradientes de esto, hace producto vectorial y te queda la normal al plano
&latex Rt(X)= \lambda (16,-4,-4) + (0,2,2) $
&latex x= 16\lambda$
&latex y= -4\lambda +2 = z$
&latex \lambda= \frac 1 6$
y lo bueno es que me queda el mismo punto A de antes o lo estoy pifiando en algo muy groso o esta bien.
Hola a todos!
Necesitaría saber como llegaron a que la ED es fi(x) – fi’(x)=0?
Mil gracias!!!
Haces el rotor de f que te queda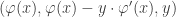
Tenés que hacer la integral doble del producto escalar entre el rotor de f y una superficie que contenga a la curva. La curva es la que te dan como
Así que elegis como superficie S:(0,1,0), ya que te dan en la ecuación de la curva un valor constante en la componente y.
Aclaro, las componentes que te puse de S, sería la normal de S.
Hola a todos!
Necesitaría saber como llegaron a que la ED es fi(x) – fi’(x)=0 en el ejercicio 2b?
Mil gracias!!!
Buenisimo, mil gracias Martin, no se habia actualizado, y en el ejercicio 4 como llegaron a que y = -x² + 4?
Millones de gracias por la ayuda!
Consulta, En el ejercicio 4 como llegaron a que y = -x² + 4?
Muchas gracias a todos!
Hola Lilian.
Para llegar a la SP de la ED lo primero que hay que hacer es reducir el orden como dice en el enunciado, entonces hacemos el siguiente reemplazo:
u = y’
u’=y»
nos queda: xu’ – u = 0
entonces escribimos a u’ como du/dx luego separamos los diferenciales y acomodamos todo para poder integrar, me quedo asi:
du/u = dx/x
integramos miembro a miembro y eso da: ln u = ln x + ln c1
por porpiedad del log unimos la x y la c : ln u = ln c1x
luego aplicamos e : u = c1x
Ahora debemos volver para atras con la reducción, escribimos a la u como y’ o para que nos quede mas comodo dy/dx, entonces:
dy/dx = c1x => dy = c1x dx =>integrando=> y = (c1x^2)/2 + c2
Ahora bien, en el enunciado tenemos dos datos f(1)=3 y f'(1)= -2
con estos datos averiguas c1 y c2 (c1 = -2 y c2 = 4)
y resulta la SP es: y = -x^2 + 4
calculo que los demas lo hicieron de la misma manera. saludos.
Muchisimas gracias Fede!!!