Este post lo dejo creado para que puedan escribir en los comentarios las consultas que tengas sobre los ejercicios.
Recordá que podés escribir fórmulas usando comandos latex, por ejemplo si escribís $latex \int_0^1 x^2 dx $ se ve como , y siempre podés previsualizar el comentario para ver si quedó bien.
Para previsualizar una fórmula escrita en podés utilizar esta página.



Hola Damian,
Resolvi este ejercicio de parcial.
Estudiar la continuidad, derivabilidad y diferenciabilidad en (0,0) de:
Mi solucion:

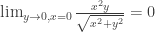
sigo pensando que es discontinua, por lo tanto voy a acercarme a (0,0) por la recta y=x.

No es continua los limites son diferentes y no es diferenciable.
Pero eso no quita que no tenga derivadas parciales así es que, trato de hallarlas.
Por el resultado de los limites anteriores podria decir que es derivable en (0,0).
Hola Pablo,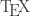 🙂
🙂
Primero que nada quedé sorprendido por el buen manejo que hacés de los comandos
Con respecto a la continuidad, cometés un error cuando te aproximás por ya que en el denominador haces
ya que en el denominador haces 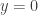 en vez de
en vez de 
Sugerencia: intentá cambiando a polares para analizar la continuidad.
Las derivadas parciales las hacés bien, pero ojo que eso no implica que la función sea derivable, para estar seguro tendrías que hacer las derivadas direccionales (se dice que es derivable si lo es en toda dirección no solo en las canónicas)
Saludos,
Damián.
Hola Damian,
Si es cierto, si voy a polares el limite me da igual a cero, entonces seria continua.
Si es que esta bien, resuelto el siguiente limite.
Por el tema diferenciabilidad voy a estudiar mas teoria.
Hola Pablo,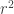 del numerador con los
del numerador con los 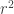 que están en la raíz cuadrada, primero tenés que sacar
que están en la raíz cuadrada, primero tenés que sacar 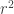 factor común del denominador y después sacarlo de la raíz, en definitiva solo se puede simplificar
factor común del denominador y después sacarlo de la raíz, en definitiva solo se puede simplificar  , pero el resto estaría bien y llegás a 0 igual.
, pero el resto estaría bien y llegás a 0 igual.
Aparentemente el comando de latex \cancel{} no funciona en wordpress, igual por el comando que pusistes me doy cuenta que hay un error ya que simplificás el
Acordate que te falta analizar las derivadas direccionales también.
Saludos,
Damián.
Hola Damian,
Retomando el ejercicio:
Aplico la definicion de derivada direccional al punto Po=(0,0) y un versor generico u=(h,k)
EL limite es igual a cero, sin importar los vectores. El limite existe y es diferenciable en todas direcciones en las cercanias del (0,0).
Esta bien ?
Hola Pablo,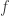 ).
).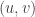 y al parámetro del límite
y al parámetro del límite 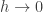
 equivale a
equivale a 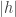
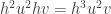
En el tercer paso se te mezclaron algunas cosas (fijate que todavía tenés la
Yo prefiero llamar al versor
Fijate que el denominador por ser
El numerador equivale a
Juntando todo queda el límite
que equivale a
Si te acercás por
Si te acercás por
Y por eso el límite existe, vale 0, y es DERIVABLE (no diferenciable) en todas direcciones en el punto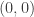
Una pregunta, usás algún software para ver las ecuaciones en latex antes de postearlas?
Saludos,
Damián.
Hola Damian,
Muchas gracias, por la aclaraciones.
Antes de postear las ecuaciones en latex, ingreso al siguiente link:
http://www.sitmo.com/latex/
Y de los siguientes link, saco algunos comandos que no encuentro en el link precedente.
http://es.wikipedia.org/wiki/LaTeX
http://rinconmatematico.com/instructivolatex/formulas.htm
Saludos.
Pablo.
Muy bueno el enlace que permite previsualizar fórmulas latex, lo agregué al post. Lástima wordpress no me deja insertar javascript sinó podría incluirlo en la barra lateral del blog.
Hola Damian,
Resolvi este ejercicio de parcial.
Dice:
Analice la derivabilidad en distintas direcciones de:
Es diferenciable esta funcion ?.
Mi solucion:
Empiezo buscando la continuidad.
Por el eje X:
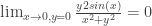
Por el eje Y:

Utilizo coordenadas polares.
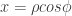

Voy a utilizar x=-y
No estoy de acuerdo con el resultado, porque no seria continua y por ello no cumple la condicion necesaria de
diferenciabilidad.
Ahora podria ver, si es derivable. (Aplico definicion)

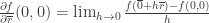
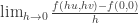
En el origen y un vector generico r
Tengo una indeterminacion, creo que me equivoque, pero no lo veo.
Hola Pablo, y que multiplicando y diviendo por
y que multiplicando y diviendo por  te va a quedar un
te va a quedar un  .
.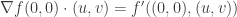 y no parece ser el caso.
y no parece ser el caso.
Primero, fijate que no te pedían continuidad, eso a lo sumo te va a servir para probar que no es diferenciable. Venías bien hasta lo de polares, después no cierra del todo lo que hicistes que te dió infinito pero está mal. Volvé a hacerlo con polares despacio y te tiene que dar que es contínua, así que no te sirve tampoco para ver si es o no diferenciable.
La parte de derivabilidad está bastante bien, pero llegás ahí y no sabés como seguir, fijate que
La diferenciabilidad la podés sacar usando que si es diferenciable tiene que cumplir
Saludos,
Damián.
pd: completé los tags latex que te olvidastes.
Damian,
Perdon,
A veces me olvido de poner al principio de una linea, la palabra «\latex» y no me parsea el string.
Como en el ejercicio anterior. La proxima miro mejor antes de Enviar.
Pablo.
Damian ,gracias por la aclaracion.
Es verdad no pedian la continuidad, pero se, de la teoria que si no es continua,
no es diferenciable, pero se ve, que al apurarme, hice mal el limite.
Volvi a reacer el limite con polares y me dio igual a cero
sin importar la
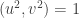
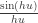
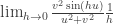
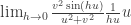

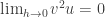
direccion del vector (u,v). Entonces es continua.
Luego, con la derivabilidad, segui los pasos que indicastes,
Mutiplico y divido por u:
El lim deveria dar:
Entonces, v=0 v u=0

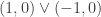
Posibles combinaciones, para que la funcion sea derivable.:
Diferenciabilidad:


Entonces se cumpliria esta igualdad:

Cuando:

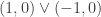
Solo seria diferenciable para esos casos.
Hola Pablo, .
.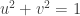 , eso viene por el hecho de que
, eso viene por el hecho de que 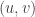 es un versor en la definición de derivadas direccionales.
es un versor en la definición de derivadas direccionales.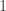 , o sea te quedaría:
, o sea te quedaría:
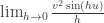

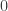 , ese límite no depende de
, ese límite no depende de 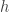 así que simplemente vale
así que simplemente vale  .
.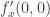 (que no es lo mismo que
(que no es lo mismo que  ) no hace falta que vuelvas a usar la definición, simplemente reemplazás
) no hace falta que vuelvas a usar la definición, simplemente reemplazás  en la expresión de las derivadas direccionales, por ejemplo en este caso
en la expresión de las derivadas direccionales, por ejemplo en este caso 
La parte de derivabilidad no está bien.
Tenés que tener mucho mas cuidado con la notación, por ejemplo, no se a que te referís con que
Creo que te confundistes con lo que te dije de que
La idea era que en el paso siguiente no lo pongas en el denominador total vale
ese límite lo hacés bien hasta:
pero no se porqué igualás eso a
Al quedarte mal las derivadas direccionales, arrastrás el error a la parte de diferenciabilidad.
De todas formas, una cosa que deberías darte cuenta es que una vez que hicistes las derivadas direccionales, si querés obtener
Consejo: cuando sospechás que algo no cierra del todo antes de avanzar con el paso siguiente revisá bien el paso actual, sinó arrastrás el error a los pasos siguientes, y tené más cuidado con la notación y con las definiciones.
Bueno, espero que te haya aclarado varias dudas,
Saludos,
Damián.
Hola Damian,
En la resolulcion del siguiente ejercicio, me encontre con siguientes inconvenientes,
Sea
 de ecuacion:
de ecuacion:
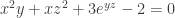 en el punto
en el punto
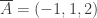

plano tangente a la superficie
Halle la ecuacion cartesiana del plano normal a la curva C en A.
Sabiendo que C esta incluida en
y en el plano de la ec. Z=2.
Para resolver el ejercicio, hay que llegar a

Con eso obtengo el plano normal.
Para hallar f'(to) , es la ec derivada de la ec implicita.
Lo que no se como obtener es, f(to). Para mi, f(to) es el vector posicion
del punto A.
Y no tengo ni idea de como utilizar, el dato del plano z=2. (Lo mas comico, es que z=2
deve ser un dato relevante).
Mas que nada quisiera saber en cual de esos pasos me equivoque, para poder rehacer el ejercicio.
Muchas gracias.
Pablo.
Hola Pablo,
Como la curva es la intersección de dos planos se tratará a lo sumo de una recta, cuyo vector director podés sacar multiplicando vectorialmente las normales de los otros dos planos.
Sabiendo que el gradiente es perpendicular al conjunto de nivel podés sacar los vectores normales a los dos planos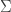 y
y  .
.
Una vez que tenés la recta, usas su vector director y punto para construir el plano normal a esa recta en ese punto.
No hace falta usar derivada implícita.
Saludos,
Damián.
buenas queria saber si pueden pasarme la resolucion del ejercicio 6 de la guia 6. es una demostracion. gracias
Hola Nestor,
Acá está:
Saludos,
Damián.
Hola Damian,
Una consulta:
Si una z=f(x,y) es diferenciable, entonces admite plano tangente y significaria que admite derivadas parciales en cualguier direccion.
Y el resultado de esas derivadas parciales puede ser diferente ?
Digo porque no entiendo bien, como interpretar el siguiente ejericio.
Considere f diferenciable en A y calcule f'(A, (3,2)) sabiendo que
f'(A, (8,6))=4 y que f'(A, (1,3))=6
Para la resolucion solo veo, operaciones basicas con los vectores (8,6)
y (1,3), pero nunca llego al vector (3,2). No se como resolverlo.
Hola Pablo, que es lo que hay que aplicar en ese ejercicio.
que es lo que hay que aplicar en ese ejercicio.

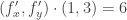

Está bien lo que decís hasta lo de «derivadas parciales en cualquier dirección», creo que quisistes decir derivadas direccionales en cualquier dirección, lo cual incluye a las derivadas parciales, es decir las direcciones canónicas.
El resultado de las derivadas puede ser diferente aunque sea diferenciable, lo único que tiene que cumplir si o si es
Es decir te quedaría
con eso te queda un sistema de dos por dos de donde sacas
Luego teniendo eso que es el gradiente es fácil sacar la derivada que te pide haciendo el producto escalar del gradiente por el vector.
Saludos,
Damián.
Damian,
Si, quise decir eso, que las derivadas parciales canonicas, son un caso de las derivadas direccionales.
Si ese vector el (3,2), que esta contenido en el plano tangente (cuyo vector director es el gradiente), entonces el producto escalar no deveria ser igual a cero ?

Digo porque, me dio este resultado:
Al hacer el producto escalar.
Gracias por tus respuestas.
Saludos,
Pablo.
Pablo,

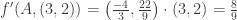
El gradiente da
Al hacer el producto escalar queda
No tiene porque dar cero, creo que te estás confundiendo con que el gradiente es normal al conjunto de nivel.
Saludos,
Damián.
Damian no se como resolver el siguiente ejercicio el E4) del primer parcial de fecha 1/6/09 que posteste vos (no se como paremetrizar la curva xq me qda algo raro).
Saludos
Hola Fede,
En ese ejercicio no pide que parametrices la curva, lo que necesitás es el plano normal a la curva en un punto. La curva te la dan como intersección de dos superficies que te dan a con ecuaciones implícitas.
Para sacar el vector tangente a la curva lo podés hacer como el producto vectorial de los gradientes de los campos escalares que definen a dichas superficies como conjuntos de nivel. (Acordate que el gradiente es perpendicular al conjunto de nivel).
Saludos,
Damián.
Hola Damián: puede ser que la guia tenga un error en la rta del pto 1 a del TP 7. A mi me da (x,y)=(t,t^2) para el sentido positivo, y (x, y)=(-t,t^2) para el sentido negativo.
Gracias!!
Andrea
Hola Andrea,
La respuesta de la guía está bien. Para saber si está bien el tuyo faltaría que me digas el intervalo en que definís la parametrización.
Acordate que hay infinitas formas distintas de parametrizar una misma curva (incluso en el mismo sentido), así que la respuesta de la guía no es la única correcta posible.
Saludos,
Damián.
Ah! claro puede haber varias respuestas!! En mi caso el intervalo es -2 <= t <= 1 para el sentido negativo, y me quedo (x,y)=(-t,t^2) .
Gracias! Damián!
Andrea
Ahora sí, tu parametrización también es correcta. 🙂
Hola Dami, estoy practicando con un final del 06/03/2008 y no me sale el pto 2)b)
Sea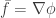 , si
, si 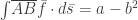
 , ¿existe (a,b) para que
, ¿existe (a,b) para que  sea maxima ?
sea maxima ?
y
como f es campo de gradientes obtuve la circulacion CB pero luego no se como seguir…. pense obtener ptos criticos (me queda una circunferencia alrededor de 1/2, -1/2 ) pero no tengo como calcular el hessiano para determinar si es max o min…
Gracias!
Hola Andrea,
No entendí que circunferencia te queda, ni porqué no podés calcular el hessiano:
La función a maximizar como bien decís es

Criterio de la derivada primera:

el único punto crítico es:
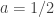
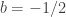
Ahora calculo el hessiano:
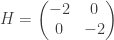
 hay extremo y como
hay extremo y como  hay un máximo relativo.
hay un máximo relativo.
Como
Por lo tanto:
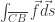 tiene un máximo relativo para
tiene un máximo relativo para 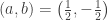
Damián, ahí me quedó más claro! Muchas gracias!
Lo que estaba tratando de calcular era anular h(a,b), con eso obtenía todos los puntos críticos, pero tenés razón, es h(a,b) al que hay calcularle el máximo.
Gracias!
Dami, te pregunto otra cosa por favor, sobre el ejercicio 1)b del final 06/03/08
Halle la ec cartesiana de la linea de campo de f que pasa por (1,2) siendo f(x,y)=(x, y-x)
Para hallar la linea de campo hago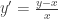
queda como es una ED exacta, la resuelvo obteniendo la funcion potencial, no?
como es una ED exacta, la resuelvo obteniendo la funcion potencial, no?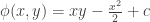
me quedaria
¿es correcto decir que si igualo eso a una constante k obtengo la linea de campo? me confundo porque el potencial hallado seria las lineas equipotenciales?….
si hago como pasa por (1,2) obtengo que k=3/2 + c
como pasa por (1,2) obtengo que k=3/2 + c
y termina dando como resultado
Gracias!!!
Andrea,
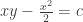
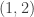 sale que
sale que  y por ende
y por ende

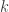 .
.
La solución de la ecuación diferencial es
como pasa por
es la línea de campo buscada, como bien encontrastes.
Lo que no hacía falta era esa otra constante
Gracias por las rtas!!
Te pregunto 2 más por favor!!
Ejercicio 1b)Final 22/07/08 , halle a para que
, halle a para que  sea maxima si
sea maxima si  con
con 
—————————
Dado
llegue a
luego no se como seguir…
Ejercicio 2b)Final 29/07/08
 con
con  es la ecuacion de una curva C incluida en la superficie F(x,y,z)=0. Analice si la recta tangente a C en A interseca al eje z, sabiendo que A=(2,4,3) pertenece a C y que
es la ecuacion de una curva C incluida en la superficie F(x,y,z)=0. Analice si la recta tangente a C en A interseca al eje z, sabiendo que A=(2,4,3) pertenece a C y que 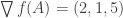
—————————
para sacar la recta tangente hice X'(t) = (1,2t,z'(t)) , en t=2 queda (1,4,z'(2)) que seria el vector director
entonces la recta me queda (x,y,z) =(2,4,3) + t(1,4,z'(2))
como es gradiente de F en A es perpendicular al vector director, es correcto lo siguiente?
(2,1,5).(1,4,z'(2))=0
con esto hallo z'(2) =-6/5
(x,y,z) =(2,4,3) + t(1,4,-6/5)
En ningun momento use el dato con (¿?)
(¿?)
Todo lo que haces parece estar bien. , no se si te piden la derivada direccional o la derivada respecto del vector
, no se si te piden la derivada direccional o la derivada respecto del vector  , de todas formas creo que la respuesta terminaría siendo la misma. El problema en ese ejercicio es que te pide maximizar, y la función que te queda
, de todas formas creo que la respuesta terminaría siendo la misma. El problema en ese ejercicio es que te pide maximizar, y la función que te queda  es una parábola «hacia abajo», es decir tiene un mínimo relativo y absoluto, pero no tiene ningún máximo.
es una parábola «hacia abajo», es decir tiene un mínimo relativo y absoluto, pero no tiene ningún máximo.
En el 1b) quedó medio ambiguo la notación de
En el 2b) lo resolvés bien, el dato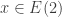 pareciera estar para indicarte que la parametrización de la curva está definida en el entorno de
pareciera estar para indicarte que la parametrización de la curva está definida en el entorno de 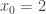 , fijate que no te dice el dominio de la parametrización, sin eso como justificás que existe
, fijate que no te dice el dominio de la parametrización, sin eso como justificás que existe 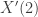 ?
?
Damian Gracias por la ayuda!!
Estoy haciendo este ejercicio del final del 04/12/08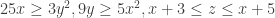
Calcule el volumen del cuerpo definido por
usando las 2 primeras ecuaciones y despues de muchos calculos llego a que

es esta la forma de hacerlo? hay alguna forma mas facil? si asi es correcto, como se sigue?
Gracias!!
Que tal, tengo una duda con el siguiente ejercicio de un parcial:
Hallar la ecuación de la recta tangente a la trayectoria ortogonal a la familia y=kx que pasa por el punto (3,4).
Pude encontrar que la familia es: x^2+y^2=25 pero al momento de hallar la recta tangente, el resultado es: (x,y)=(3,4)+s(-4,3).
De dónde sale el (-4,3)? Porque el gradiente, evaluado en (3,4) es (6,8). Cómo se relaciona con el vector director?
Mil gracias!
Hola María,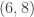 , o sea que también es un vector normal la mitad de ese vector, es decir
, o sea que también es un vector normal la mitad de ese vector, es decir 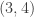 , entonces un vector tangente es
, entonces un vector tangente es  (es un truco común, dar vuelta el orden y cambiarle el signo a uno para obtener un vector perpendicular a uno dado en
(es un truco común, dar vuelta el orden y cambiarle el signo a uno para obtener un vector perpendicular a uno dado en 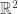 )
)
El gradiente te da un vector normal al conjunto de nivel, en este caso
Suerte.