Calcule la masa de los siguientes cuerpos:
b) cuerpo definido por 
Solución:
La función densidad es 
Como la esfera esta cortada por dos planos, voy a tomar una variante de coordenadas esféricas (que sería equivalente a rotar 
Transformo la función densidad:
Por lo tanto la masa es:
![\frac{k}{4} [-\cos(\phi)]_{\pi/4}^{3\pi/4} [\frac{\beta}{2} - \frac{\sin(2\beta)}{4}]_{0}^{\pi}](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bk%7D%7B4%7D+%5B-%5Ccos%28%5Cphi%29%5D_%7B%5Cpi%2F4%7D%5E%7B3%5Cpi%2F4%7D+%5B%5Cfrac%7B%5Cbeta%7D%7B2%7D+-+%5Cfrac%7B%5Csin%282%5Cbeta%29%7D%7B4%7D%5D_%7B0%7D%5E%7B%5Cpi%7D&bg=ffffff&fg=333333&s=0&c=20201002)
![\frac{k}{4} [\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}] [\frac{\pi}{2}]](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bk%7D%7B4%7D+%5B%5Cfrac%7B%5Csqrt%7B2%7D%7D%7B2%7D+%2B+%5Cfrac%7B%5Csqrt%7B2%7D%7D%7B2%7D%5D+%5B%5Cfrac%7B%5Cpi%7D%7B2%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002)
El siguiente es el gráfico del cuerpo:
draw3d(surface_hide=true,
xlabel = "x", ylabel = "y", zlabel = "z",
color=blue,
parametric_surface(cos(b), cos(p)*sin(b), sin(p)*sin(b), p,%pi/4,3*%pi/4, b,0,%pi),
color=light-blue,
parametric_surface(u*cos(b), u*sqrt(2)/2*sin(b), u*sqrt(2)/2*sin(b), u,0,1, b,0,%pi),
parametric_surface(u*cos(b), -u*sqrt(2)/2*sin(b), u*sqrt(2)/2*sin(b), u,0,1, b,0,%pi)
);
.
Análisis Matemático II 
Damian, yo podria proyectar ese cuerpo en el plano XY?
Intente calcular el volumen con cilindricas del lado de la Y positiva (angulo de -pi/2 a pi/2) y luego multiplicar por 2 pero no me da.
En caso de no poder, no entiendo bien el criterio para elegir el plano al cual proyectar en casos como este
gracias
gabriel
Hola Gabriel,
En este caso te conviene usar coordenadas esféricas como en la resolución, en vez de cilíndricas, a pesar de ser proyectable en el plano
Por otro lado, tené en cuenta que el ejercicio pide calcular la masa y no el volúmen, con lo cual no te conviene usar propiedades de simetría ya que además del cuerpo tendría que ser simétrica la función densidad.
Saludos,
Damián
Hola que tal?
Yo lo proyecte pero en el plano ZY y me quedaria algo asi : (><). Estando en el medio el eje Z, entonces se podrian aplicar las propiedades de simetria para la masa, (se me ocurrió, ya que varia igual para ambos lados).
El tema es que no me avive de usar esfericas y usé cilindricas. Los limites me quedaron asi: (siendo mis polares: z= ρ sen (φ) y=ρ cos (φ) ):
D1: 7/4π<=φ<=1/4π
0<=ρ<=1
-(1-ρ^2)^1/2<= x <= (1-ρ^2)^1/2
D2:3/4π<=φ<=5/4π
0<=ρ<=1
-(1-ρ^2)^1/2<= x <= (1-ρ^2)^1/2
Y Calcule la primera integral triple (D1) y me termino dando (Dps de una integral de tablas bastante fea) (k3π/16) multiplicado por 2 (por la otra semi esfera) me da (K3π/8) MUY cerca del resultado. Tengo mal algun limite?
Gracias, Aoshido.
Pd: (en el grafico dibujaste 1 de las "semiesferas" pero son las 2 no?)
Hola Aoshido,
y ningún 
real satisface eso.
, habría que hacerlo y ver si da lo mismo.
No entiendo del todo como te quedó tu región de integración.
Por un lado, a mi me queda una sola región, como si fuera un gajo de una mandarina, en el dibujo se ve bien, y no dos semiesferas.
Por otro lado, en tu región D1 ponés
De todas formas proyectar sobre el plano yz si bien no es imposible no parece ser una forma sencilla de resolver este ejercicio. Me parece que en tu caso te debería quedar una región sola, y el ángulo ir de
Suerte,
Damián.
Hola Damian,gracias por tu pronta respuesta.
Si, me exprese mal, no quise decir 2 semi-esferas, si no 2 gajos. Ya resolvi el problema, tristemente habia abierto mal el modulo, entonces me quedaban los dos «gajos» de los costados jajaja, no se como me dio tan cerca el resultado, muchas gracias por la ayuda!
Ah por cierto, es verdad lo que decis de (7/4π<=φ<=1/4π), cuando lo defini no me di cuenta, pero entendiste que región quise definir al menos? jajaja.
D1 (mal definido) era el gajo del costado derecho, pero creo que para quedara bien definido (creo) tuve que haberlo expresado como 7/4π<=φ<=9/4π.
Devuelta muchas gracias por la ayuda!
Saludos!
La verdad que no entendí como lo resolvistes. Supongo que si te da el resultado correcto las chances que esté bien son buenas, pero igual ojo cuando aplicás propiedades de simetría, yo nunca lo recomiendo cuando lo que se calcula es masa porque no alcanza con que el cuerpo sea simétrico, y no cuesta nada hacer la integral completa.
lo cual es medio extraño.
No me lograron cerrar los ángulos que tomastes,
En cilíndricas sobre el eje
te debería quedar algo así como
donde la densidad quedó como
(son todos positivos en la región del cuerpo)
donde el cambio fué
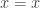
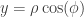
siguiendo,
![M = 2k \left[ -\cos(\phi) \right]_{\pi/4}^{3\pi/4} \int_0^1 \rho^2 \sqrt{1-\rho^2} d\rho](https://s0.wp.com/latex.php?latex=M+%3D+2k+%5Cleft%5B+-%5Ccos%28%5Cphi%29+%5Cright%5D_%7B%5Cpi%2F4%7D%5E%7B3%5Cpi%2F4%7D+%5Cint_0%5E1+%5Crho%5E2+%5Csqrt%7B1-%5Crho%5E2%7D+d%5Crho&bg=ffffff&fg=333333&s=0&c=20201002)
la integral que queda para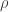
es horrible, pero se puede resolver por tabla.
De todas formas podemos verificar que da el resultado correcto usando el wolfram alpha.
Tal cual!!!
Asi me quedo la ecuacion de la masa, hice exactamente los mismos cambios, sin embargo tuve dos errores yo, abrí mal el modulo mi (region me habia quedado -y<=z<=y) por eso es que yo hablaba de "2 gajos" y ahi te queda definido el "gajo de la derecha" entre 7/4π<=φ<=9/4π.
Es verdad que la integral que quedaba era horrible yo la resolvi por tabla y aun así fue bastante molesto.
Respecto a las propiedades de simetría, no suelo aplicarlas pero la verdad que en este caso me significaba hacer 2 veces el gajo (por que yo tenia mal definida el area) por eso es que esta vez, lo utilice jajaja.
Espero ahora me haya podido expresar mejor jajaja muchisimas gracias por la ayuda!
damian una pregunta como sacas el que angulo vaya de pi/4 a 3/4pi no me quedo claro eso
Hola agustín,
. El ángulo 
parte del eje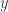 
, y se mueve hacia el eje 
.
sale que 
, pensá en el gráfico del módulo. Se puede hacer más algebráicamente pero es más trabajo.
Pensá en la proyección sobre el plano
Por la condición
Saludos,
Damián.
Hola Damian, no entiendo porque haces esa rotacion en la coordenadas esfericas, me podrias explicar. Gracias
Hola Juani,
Porque de esa forma es más sencillo. Si mirás las superficies coordenadas de esféricas te das cuenta que de esa forma quedan los intervalos de integración entre constantes, mientras que si no lo rotás es mucho más difícil (¿lo intentastes hacer sin rotar?)
Saludos,
Damián.